Space spanned by the lowest order Raviart-Thomas functions. More...

#include </home/wojtek/Projects/BEM/bempp-sven/bempp/lib/space/raviart_thomas_0_vector_space.hpp>

Inheritance diagram for Bempp::RaviartThomas0VectorSpace< BasisFunctionType >:

Public Types
typedef Space < BasisFunctionType > ::CoordinateType	CoordinateType

typedef Space < BasisFunctionType > ::ComplexType	ComplexType

typedef Base::CollectionOfShapesetTransformations	CollectionOfShapesetTransformations

typedef Base::CollectionOfBasisTransformations	CollectionOfBasisTransformations

Public Types inherited from Bempp::Space< BasisFunctionType >
typedef Fiber::ScalarTraits < BasisFunctionType > ::RealType	CoordinateType
	Type used to represent coordinates.

typedef Fiber::ScalarTraits < BasisFunctionType > ::ComplexType	ComplexType
	Equivalent to std::complex<CoordinateType>.

typedef Fiber::CollectionOfShapesetTransformations < CoordinateType >	CollectionOfShapesetTransformations
	Appropriate instantiation of Fiber::CollectionOfShapesetTransformations.

typedef Fiber::CollectionOfBasisTransformations < CoordinateType >	CollectionOfBasisTransformations
	Appropriate instantiation of Fiber::CollectionOfBasisTransformations.

Public Member Functions
	RaviartThomas0VectorSpace (const shared_ptr< const Grid > &grid, bool putDofsOnBoundaries=false)
	Constructor. More...

	RaviartThomas0VectorSpace (const shared_ptr< const Grid > &grid, const GridSegment &segment, bool putDofsOnBoundaries=false, int dofMode=EDGE_ON_SEGMENT)
	Constructor. More...

virtual shared_ptr< const Space< BasisFunctionType > >	discontinuousSpace (const shared_ptr< const Space< BasisFunctionType > > &self) const
	Return a shared pointer to an appropriate counterpart to this space, with basis functions extending only over single elements. More...

virtual bool	isDiscontinuous () const
	Return true if each basis function of this space extends over only a single element, false otherwise.

virtual const CollectionOfShapesetTransformations &	basisFunctionValue () const
	Transformation mapping shape functions to basis functions. More...

virtual int	domainDimension () const
	Dimension of the grid on which functions from this space are defined.

virtual int	codomainDimension () const
	Dimension of the codomain of the functions. More...

virtual bool	isBarycentric () const
	Return `true` if space is based on a barycentric refinement.

virtual bool	spaceIsCompatible (const Space< BasisFunctionType > &other) const
	Return true if `other` is compatible to this space, i.e. the global dofs of the two spaces agree with each other.

virtual SpaceIdentifier	spaceIdentifier () const
	Return the identifier of the space.

virtual ElementVariant	elementVariant (const Entity< 0 > &element) const
	Return the variant of element `element`. More...

virtual void	setElementVariant (const Entity< 0 > &element, ElementVariant variant)
	Set the variant of element `element` to `variant`. More...

virtual const Fiber::Shapeset < BasisFunctionType > &	shapeset (const Entity< 0 > &element) const
	Reference to the shapeset attached to the specified element.

virtual size_t	globalDofCount () const
	Number of global degrees of freedom.

virtual size_t	flatLocalDofCount () const
	Total number of local degrees of freedom on all elements.

virtual void	getGlobalDofs (const Entity< 0 > &element, std::vector< GlobalDofIndex > &dofs, std::vector< BasisFunctionType > &dofWeights) const
	Map local degrees of freedom residing on an element to global degrees of freedom. More...

virtual void	global2localDofs (const std::vector< GlobalDofIndex > &globalDofs, std::vector< std::vector< LocalDof > > &localDofs, std::vector< std::vector< BasisFunctionType > > &localDofWeights) const

virtual void	flatLocal2localDofs (const std::vector< FlatLocalDofIndex > &flatLocalDofs, std::vector< LocalDof > &localDofs) const
	Map flat indices of local degrees of freedom to local degrees of freedom. More...

virtual void	getGlobalDofPositions (std::vector< Point3D< CoordinateType > > &positions) const
	Retrieve the reference positions of global degrees of freedom. More...

virtual void	getFlatLocalDofPositions (std::vector< Point3D< CoordinateType > > &positions) const
	Retrieve the reference positions of local degrees of freedom ordered by their flat index. More...

virtual void	getGlobalDofBoundingBoxes (std::vector< BoundingBox< CoordinateType > > &bboxes) const
	Retrieve bounding boxes of global degrees of freedom. More...

virtual void	getFlatLocalDofBoundingBoxes (std::vector< BoundingBox< CoordinateType > > &bboxes) const
	Retrieve bounding boxes of local degrees of freedom ordered by their flat index. More...

virtual void	getGlobalDofNormals (std::vector< Point3D< CoordinateType > > &normals) const
	Retrieve the unit vectors normal to the grid at the positions of global degrees of freedom. More...

virtual void	getFlatLocalDofNormals (std::vector< Point3D< CoordinateType > > &normals) const
	Retrieve the unit vectors normal to the grid at the positions of global degrees of freedom. More...

virtual void	dumpClusterIds (const char *fileName, const std::vector< unsigned int > &clusterIdsOfGlobalDofs) const
	Write a VTK file showing the distribution of global or flat local degrees of freedom into clusters. More...

virtual void	dumpClusterIdsEx (const char *fileName, const std::vector< unsigned int > &clusterIdsOfGlobalDofs, DofType dofType) const
	Write a VTK file showing the distribution of global or flat local degrees of freedom into clusters. More...

Public Member Functions inherited from Bempp::Space< BasisFunctionType >
	Space (const shared_ptr< const Grid > &grid)
	Constructor. More...

	Space (const Space< BasisFunctionType > &other)
	Copy Constructor.

virtual	~Space ()
	Destructor.

Space< BasisFunctionType > &	operator= (const Space< BasisFunctionType > &other)
	Assignment operator.

shared_ptr< GeometryFactory >	elementGeometryFactory () const
	Return the GeometryFactory associated with the mesh.

BEMPP_DEPRECATED void	assignDofs ()
	Assign global degrees of freedom to local degrees of freedom. More...

BEMPP_DEPRECATED bool	dofsAssigned () const
	True if global degrees of freedom have been already assigned to local degrees of freedom, false otherwise. More...

virtual void	getGlobalDofs (const Entity< 0 > &element, std::vector< GlobalDofIndex > &dofs) const
	Map local degrees of freedom residing on an element to global degrees of freedom. More...

virtual bool	gridIsIdentical (const Space< BasisFunctionType > &other) const
	Return true if both spaces act on the same grid.

virtual void	global2localDofs (const std::vector< GlobalDofIndex > &globalDofs, std::vector< std::vector< LocalDof > > &localDofs) const
	Map global degrees of freedom to local degrees of freedom. More...

virtual void	getGlobalDofInterpolationPoints (arma::Mat< CoordinateType > &points) const
	Retrieve the interpolation points of the global degrees of freedom. More...

virtual void	getNormalsAtGlobalDofInterpolationPoints (arma::Mat< CoordinateType > &normals) const
	Retrieve the unit vectors normal to the grid at the interpolation points of the global degrees of freedom. More...

virtual void	getGlobalDofInterpolationDirections (arma::Mat< CoordinateType > &directions) const
	Retrieve the interpolation directions of the global degrees of freedom. More...

shared_ptr< const Grid >	grid () const
	Shared pointer to the grid on which the functions from this space are defined.

virtual BEMPP_DEPRECATED const Fiber::Basis < BasisFunctionType > &	basis (const Entity< 0 > &element) const
	Reference to the shapeset attached to the specified element. More...

virtual BEMPP_DEPRECATED const CollectionOfBasisTransformations &	shapeFunctionValue () const
	Transformation mapping shape functions to basis functions. More...

virtual shared_ptr< const Space< BasisFunctionType > >	barycentricSpace (const shared_ptr< const Space< BasisFunctionType > > &self) const
	Return an equivalent space (in terms of global Dofs), but defined using local dofs on the barycentrically refined grid.

unsigned int	level () const
	Return the grid level of the current space.

int	gridDimension () const
	Return the underlying grid dimension.

int	worldDimension () const
	Return the underlying world dimension.

const GridView &	gridView () const
	Return the grid view of the current space.

Private Types
typedef Space< BasisFunctionType >	Base

Private Member Functions
void	initialize ()

void	assignDofsImpl ()

Additional Inherited Members
Related Functions inherited from Bempp::Space< BasisFunctionType >
template<typename BasisFunctionType >
void	getAllShapesets (const Space< BasisFunctionType > &space, std::vector< const Fiber::Shapeset< BasisFunctionType > * > &shapesets)
	Get pointers to Basis objects corresponding to all elements of the grid on which a function space is defined. More...

template<typename BasisFunctionType >
void BEMPP_DEPRECATED	getAllBases (const Space< BasisFunctionType > &space, std::vector< const Fiber::Basis< BasisFunctionType > * > &bases)
	Get pointers to Basis objects corresponding to all elements of the grid on which a function space is defined. More...

template<typename BasisFunctionType >
int	maximumShapesetOrder (const Space< BasisFunctionType > &space)
	Return the maximum polynomial order of the shapesets defined by `space` on the elements of the space's underlying grid.

Detailed Description

template<typename BasisFunctionType>
class Bempp::RaviartThomas0VectorSpace< BasisFunctionType >

Space spanned by the lowest order Raviart-Thomas functions.

On boundaries between elements, the functions from this space have continuous normal components.

Constructor & Destructor Documentation

template<typename BasisFunctionType >

Bempp::RaviartThomas0VectorSpace< BasisFunctionType >::RaviartThomas0VectorSpace	(	const shared_ptr< const Grid > &	grid,
		bool	putDofsOnBoundaries = `false`
	)

explicit

Constructor.

Parameters

[in]	grid	Grid on which the functions from the newly constructed space will be defined.
[in]	putDofsOnBoundaries	If set to `false` (default), degrees of freedom will not be placed on edges lying on boundaries of the grid. This is usually the desired behaviour for simulations of open perfectly conducting surfaces (sheets). If set to `true`, degrees of freedom will be placed on all edges belonging to the chosen segment of the grid.

template<typename BasisFunctionType >

Bempp::RaviartThomas0VectorSpace< BasisFunctionType >::RaviartThomas0VectorSpace	(	const shared_ptr< const Grid > &	grid,
		const GridSegment &	segment,
		bool	putDofsOnBoundaries = `false`,
		int	dofMode = `EDGE_ON_SEGMENT`
	)

Constructor.

Parameters

[in]	grid	Grid on which the functions from the newly constructed space will be defined.
[in]	segment	Segment of the grid on which the space should be defined.
[in]	putDofsOnBoundaries	If set to `false` (default), degrees of freedom will not be placed on edges lying on boundaries of the grid. This is usually the desired behaviour for simulations of open perfectly conducting surfaces (sheets). If set to `true`, degrees of freedom will be placed on all edges belonging to the chosen segment of the grid.
[in]	dofMode	If set to EDGE_ON_SEGMENT (default), degrees of freedom will be placed on the edges belonging to `segment`. If set to ELEMENT_ON_SEGMENT, degrees of freedom will be placed on the edges adjacent to at least one element belonging to `segment`. (This distinction is important for example if `segment` was constructed as the intersection of two closed domains; such an intersection may contain no elements, but only some vertices and edges).

Member Function Documentation

template<typename BasisFunctionType >

const RaviartThomas0VectorSpace< BasisFunctionType >::CollectionOfShapesetTransformations & Bempp::RaviartThomas0VectorSpace< BasisFunctionType >::basisFunctionValue ( ) const

virtual

Transformation mapping shape functions to basis functions.

This function returns a CollectionOfShapesetTransformations object consisting of a single transformation that maps values of shape functions defined on a reference element to those of basis functions defined on a particular element of the grid.

This transformation is the identity for spaces of scalar-valued functions, but may be more complicated for spaces of vector-valued functions, e.g. 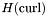$H(\mathrm{curl})$ .

Reimplemented from Bempp::Space< BasisFunctionType >.

template<typename BasisFunctionType >

int Bempp::RaviartThomas0VectorSpace< BasisFunctionType >::codomainDimension ( ) const

virtual

Dimension of the codomain of the functions.

In other words, number of components of the values of the functions. (E.g. H1 space -> 1, H(curl) space on a 2D surface -> 2).

Implements Bempp::Space< BasisFunctionType >.

template<typename BasisFunctionType >

shared_ptr< const Space< BasisFunctionType > > Bempp::RaviartThomas0VectorSpace< BasisFunctionType >::discontinuousSpace ( const shared_ptr< const Space< BasisFunctionType > > & self ) const

virtual

Return a shared pointer to an appropriate counterpart to this space, with basis functions extending only over single elements.

Let 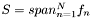$S = span_{n=1}^N f_n$ denote the function space represented by this object, with 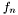$f_n$ its basis functions.

If the functions 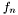$f_n$ are scalar-valued, discontinuousSpace() should return a shared pointer to an object representing a space 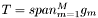$T = span_{m=1}^M g_m$ with basis functions 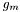$g_m$ such that:

.
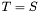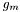The support of each basis function is a single element.
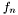Each function has a unique representation in the basis of 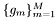$\{g_m\}_{m=1}^M$ and each function 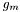contributes to exactly one function .

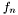If the values of functions 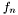$f_n$ are vectors with 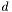$d$ components, discontinuousSpace() should return a shared pointer to an object representing a space 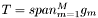$T = span_{m=1}^M g_m$ of with scalar-valued basis functions 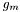$g_m$ such that

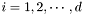For each $i = 1, 2, \cdots, d$ it holds that 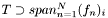$T \supset span_{n=1}^N (f_n)_i$ , where 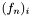denotes the 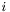th component of .
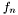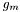The support of each basis function is a single element.

Parameters

[in] self This must be a shared pointer to *this.

Implements Bempp::Space< BasisFunctionType >.

template<typename BasisFunctionType >

void Bempp::RaviartThomas0VectorSpace< BasisFunctionType >::dumpClusterIds	(	const char *	fileName,
		const std::vector< unsigned int > &	clusterIdsOfGlobalDofs
	)		const

virtual

Write a VTK file showing the distribution of global or flat local degrees of freedom into clusters.

Parameters

[in]	fileName	Name of the VTK file to be created (without extension).
[in]	clusterIdsOfGlobalDofs	Vector whose ith element contains the identifier of the cluster to which ith global degree of freedom has been assigned.

This function generates a VTK file containing a single data series mapping the ``positions'' (see getGlobalDofPositions()) of global degrees of freedom to the identifiers of the clusters to which these degrees of freedom have been assigned. It is intended for debugging clustering algorithms.

Deprecated:: This function is deprecated. Use dumpClusterIdEx() instead, which supports dumping of cluster identifiers of flat local degrees of freedom in addition to the global ones.

Implements Bempp::Space< BasisFunctionType >.

template<typename BasisFunctionType >

void Bempp::RaviartThomas0VectorSpace< BasisFunctionType >::dumpClusterIdsEx	(	const char *	fileName,
		const std::vector< unsigned int > &	clusterIdsOfGlobalDofs,
		DofType	dofType
	)		const

virtual

Write a VTK file showing the distribution of global or flat local degrees of freedom into clusters.

Parameters

[in]	fileName	Name of the VTK file to be created (without extension).
[in]	clusterIdsOfGlobalDofs	Vector whose ith element contains the identifier of the cluster to which ith degree of freedom has been assigned.
[in]	dofType	Type of degrees of freedom (GLOBAL_DOFS or FLAT_LOCAL_DOFS).

This function generates a VTK file containing a single data series mapping the ``positions'' (see getGlobalDofPositions() and getFlatLocalDofPositions()) of the chosen type of degrees of freedom to the identifiers of the clusters to which these degrees of freedom have been assigned. It is intended for debugging clustering algorithms.

This function supersedes dumpClusterIds().

Reimplemented from Bempp::Space< BasisFunctionType >.

template<typename BasisFunctionType >

ElementVariant Bempp::RaviartThomas0VectorSpace< BasisFunctionType >::elementVariant ( const Entity< 0 > & element ) const

virtual

Return the variant of element element.

Possible return values:

3: triangular element,
4: quadrilateral element.

Implements Bempp::Space< BasisFunctionType >.

References Bempp::Entity< 0 >::type().

template<typename BasisFunctionType >

void Bempp::RaviartThomas0VectorSpace< BasisFunctionType >::flatLocal2localDofs	(	const std::vector< FlatLocalDofIndex > &	flatLocalDofs,
		std::vector< LocalDof > &	localDofs
	)		const

virtual

Map flat indices of local degrees of freedom to local degrees of freedom.

Parameters

[in]	flatLocalDofs	Vector containing flat indices of local degrees of freedom.
[out]	localDofs	Vector whose `i`th element is the local degree of freedom with flat index given by `flatLocalDofs[i]`.

Implements Bempp::Space< BasisFunctionType >.

References Bempp::acc().

template<typename BasisFunctionType >

void Bempp::RaviartThomas0VectorSpace< BasisFunctionType >::getFlatLocalDofBoundingBoxes ( std::vector< BoundingBox< CoordinateType > > & boundingBoxes ) const

virtual

Retrieve bounding boxes of local degrees of freedom ordered by their flat index.

Parameters

[out] boundingBoxes Vector whose ith element contains the bounding box the local degree of freedom with flat index i.

Note: This function is intended as a helper for clustering algorithms used in matrix compression algorithms such as adaptive cross approximation.

Reimplemented from Bempp::Space< BasisFunctionType >.

References Bempp::acc(), Bempp::IndexSet::entityIndex(), Bempp::Entity< 0 >::geometry(), Bempp::Geometry::getCorners(), Bempp::BoundingBox< CoordinateType >::lbound, and Bempp::BoundingBox< CoordinateType >::ubound.

template<typename BasisFunctionType >

void Bempp::RaviartThomas0VectorSpace< BasisFunctionType >::getFlatLocalDofNormals ( std::vector< Point3D< CoordinateType > > & normals ) const

virtual

Retrieve the unit vectors normal to the grid at the positions of global degrees of freedom.

Parameters

[out] normals Vector whose ith element contains the unit vector normal to the grid at the reference position of the local degree of freedom with flat index i.

Reimplemented from Bempp::Space< BasisFunctionType >.

References Bempp::IndexSet::entityIndex(), Bempp::Entity< 0 >::geometry(), and Bempp::Geometry::getNormals().

template<typename BasisFunctionType >

void Bempp::RaviartThomas0VectorSpace< BasisFunctionType >::getFlatLocalDofPositions ( std::vector< Point3D< CoordinateType > > & positions ) const

virtual

Retrieve the reference positions of local degrees of freedom ordered by their flat index.

Parameters

[out] positions Vector whose ith element contains the coordinates of the point taken to be the ``reference position'' (in some sense) of the local degree of freedom with flat index i.

Note: This function is intended as a helper for clustering algorithms used in matrix compression algorithms such as adaptive cross approximation.

Implements Bempp::Space< BasisFunctionType >.

References Bempp::acc().

template<typename BasisFunctionType >

void Bempp::RaviartThomas0VectorSpace< BasisFunctionType >::getGlobalDofBoundingBoxes ( std::vector< BoundingBox< CoordinateType > > & boundingBoxes ) const

virtual

Retrieve bounding boxes of global degrees of freedom.

Parameters

[out] boundingBoxes Vector whose ith element contains the bounding box of ith global degree of freedom.

Note: This function is intended as a helper for clustering algorithms used in matrix compression algorithms such as adaptive cross approximation.

Reimplemented from Bempp::Space< BasisFunctionType >.

template<typename BasisFunctionType >

void Bempp::RaviartThomas0VectorSpace< BasisFunctionType >::getGlobalDofNormals ( std::vector< Point3D< CoordinateType > > & normals ) const

virtual

Retrieve the unit vectors normal to the grid at the positions of global degrees of freedom.

Parameters

[out] normals Vector whose ith element contains the unit vector normal to the grid at the reference position of ith global degree of freedom.

Reimplemented from Bempp::Space< BasisFunctionType >.

References Bempp::acc(), Bempp::IndexSet::entityIndex(), Bempp::Entity< 0 >::geometry(), and Bempp::Geometry::getNormals().

template<typename BasisFunctionType >

void Bempp::RaviartThomas0VectorSpace< BasisFunctionType >::getGlobalDofPositions ( std::vector< Point3D< CoordinateType > > & positions ) const

virtual

Retrieve the reference positions of global degrees of freedom.

Parameters

[out] positions Vector whose ith element contains the coordinates of the point taken to be the "reference position" (in some sense) of ith global degree of freedom.

Note: This function is intended as a helper for clustering algorithms used in matrix compression algorithms such as adaptive cross approximation.

Implements Bempp::Space< BasisFunctionType >.

References Bempp::acc().

template<typename BasisFunctionType >

void Bempp::RaviartThomas0VectorSpace< BasisFunctionType >::getGlobalDofs	(	const Entity< 0 > &	element,
		std::vector< GlobalDofIndex > &	dofs,
		std::vector< BasisFunctionType > &	localDofWeights
	)		const

virtual

Map local degrees of freedom residing on an element to global degrees of freedom.

Parameters

[in]	element	An element of the grid grid().
[out]	dofs	Vector whose ith element is the index of the global degrees of freedom to which the ith local degree of freedom residing on `element` contributes. A negative number means that a given local degree of freedom does not contribute to any global one.
[out]	localDofWeights	Vector whose ith element is the weight with which the ith local degree of freedom residing on `element` contributes to "its" global degree of freedom.

Reimplemented from Bempp::Space< BasisFunctionType >.

References Bempp::acc(), and Bempp::Mapper::entityIndex().

template<typename BasisFunctionType >

void Bempp::RaviartThomas0VectorSpace< BasisFunctionType >::setElementVariant	(	const Entity< 0 > &	element,
		ElementVariant	variant
	)

virtual

Set the variant of element element to variant.

The element variant determines the set of basis functions defined on the element (e.g. maximum polynomial order). Different subclasses of Space interpret the variant argument in different ways; for more information, see the documentation of these subclasses.

Note: Calling this function only makes sense for subclasses implementing adaptive function spaces. Currently there are no such subclasses.

Implements Bempp::Space< BasisFunctionType >.

The documentation for this class was generated from the following files:

/home/wojtek/Projects/BEM/bempp-sven/bempp/lib/space/raviart_thomas_0_vector_space.hpp
/home/wojtek/Projects/BEM/bempp-sven/bempp/lib/space/raviart_thomas_0_vector_space.cpp

Public Types

Public Member Functions

Private Types

Private Member Functions

Additional Inherited Members

Detailed Description

template<typename BasisFunctionType> class Bempp::RaviartThomas0VectorSpace< BasisFunctionType >

Constructor & Destructor Documentation

Member Function Documentation

template<typename BasisFunctionType>
class Bempp::RaviartThomas0VectorSpace< BasisFunctionType >