|
BEM++
2.0
|
|
BEM++
2.0
|
Abstract interface of a local assembler for integral operators. More...
#include </home/wojtek/Projects/BEM/bempp-sven/bempp/lib/fiber/local_assembler_for_integral_operators.hpp>

Public Types | |
|
typedef ScalarTraits < ResultType >::RealType | CoordinateType |
Public Member Functions | |
| virtual void | evaluateLocalWeakForms (CallVariant callVariant, const std::vector< int > &elementIndicesA, int elementIndexB, LocalDofIndex localDofIndexB, std::vector< arma::Mat< ResultType > > &result, CoordinateType nominalDistance=-1.)=0 |
| Assemble local weak forms. More... | |
| virtual void | evaluateLocalWeakForms (const std::vector< int > &testElementIndices, const std::vector< int > &trialElementIndices, Fiber::_2dArray< arma::Mat< ResultType > > &result, CoordinateType nominalDistance=-1.)=0 |
| Assemble local weak forms. More... | |
| virtual CoordinateType | estimateRelativeScale (CoordinateType minDist) const =0 |
| Estimate how fast the entries in the matrix of this operator decay with interelement distance. More... | |
Abstract interface of a local assembler for integral operators.
Let 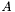 be an integral boundary operator. A local assembler associated with this operator constructs matrices
be an integral boundary operator. A local assembler associated with this operator constructs matrices 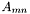 , where
, where 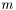 is a test element number and
is a test element number and 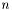 a trial element number, with entries
a trial element number, with entries  ) where
) where 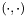 is the standard scalar product,
is the standard scalar product,  are the element-level test functions defined on element
are the element-level test functions defined on element 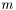 and
and 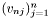 are the element-level trial functions defined on element
are the element-level trial functions defined on element 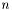 .
.
The local assembler is responsible for choosing an appropriate way of evaluating the necessary integrals.
|
pure virtual |
Estimate how fast the entries in the matrix of this operator decay with interelement distance.
This function should return a rough (!) estimate of the magnitude of the entries in the matrix of this operator associated with a pair of test and trial elements lying a distance minDist from each other, relative to the estimated magnitude of entries associated with coincident elements. If no good estimate can be given, the function can return 1.
Implemented in Fiber::DefaultLocalAssemblerForIntegralOperatorsOnSurfaces< BasisFunctionType, KernelType, ResultType, GeometryFactory >.
|
pure virtual |
Assemble local weak forms.
In this overload, a "column" of local weak forms is assembled. More specifically, on exit result is a vector of local weak forms corresponding to the following pairs of elements:
callVariant is TEST_TRIAL, all pairs (elementA, elementB) for elementA in elementsA;callVariant is TRIAL_TEST, all pairs (elementB, elementA) for elementA in elementsA.Unless localDofIndexB is set to ALL_DOFS, only entries corresponding to the (localDofIndexB)th local DOF on elementB are calculated.
If nominalDistance is nonnegative, it is taken as the distance between all element pairs for the purposes of selecting the quadrature method. Otherwise the interelement distance is calculated separately for each element pair.
Implemented in Fiber::DefaultLocalAssemblerForIntegralOperatorsOnSurfaces< BasisFunctionType, KernelType, ResultType, GeometryFactory >.
|
pure virtual |
Assemble local weak forms.
This overload constructs and assigns to the output parameter result the 2D array of local weak forms corresponding to all pairs (testElement, trialElement) with testElement in testElementIndices and trialElement in trialElementIndices.
This function should be used primarily for small blocks of elements lying close to each other.
If nominalDistance is nonnegative, it is taken as the distance between all element pairs for the purposes of selecting the quadrature method. Otherwise the interelement distance is calculated separately for each element pair.
Implemented in Fiber::DefaultLocalAssemblerForIntegralOperatorsOnSurfaces< BasisFunctionType, KernelType, ResultType, GeometryFactory >.
 1.8.5
1.8.5