An integral representing the weak form of an integral operator. More...

#include </home/wojtek/Projects/BEM/bempp-sven/bempp/lib/fiber/test_kernel_trial_integral.hpp>

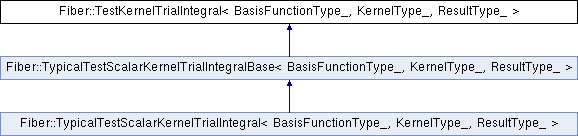
Inheritance diagram for Fiber::TestKernelTrialIntegral< BasisFunctionType_, KernelType_, ResultType_ >:

Public Types
typedef BasisFunctionType_	BasisFunctionType

typedef KernelType_	KernelType

typedef ResultType_	ResultType

typedef ScalarTraits < ResultType >::RealType	CoordinateType

Public Member Functions
virtual	~TestKernelTrialIntegral ()
	Destructor.

virtual void	addGeometricalDependencies (size_t &testGeomDeps, size_t &trialGeomDeps) const =0
	Retrieve types of geometrical data on which the integrand of this integral depends explicitly. More...

virtual void	evaluateWithTensorQuadratureRule (const GeometricalData< CoordinateType > &testGeomData, const GeometricalData< CoordinateType > &trialGeomData, const CollectionOf3dArrays< BasisFunctionType > &testTransformations, const CollectionOf3dArrays< BasisFunctionType > &trialTransformations, const CollectionOf4dArrays< KernelType > &kernels, const std::vector< CoordinateType > &testQuadWeights, const std::vector< CoordinateType > &trialQuadWeights, arma::Mat< ResultType > &result) const =0
	Evaluate the integral using a tensor-product quadrature rule. More...

virtual void	evaluateWithNontensorQuadratureRule (const GeometricalData< CoordinateType > &testGeomData, const GeometricalData< CoordinateType > &trialGeomData, const CollectionOf3dArrays< BasisFunctionType > &testTransformations, const CollectionOf3dArrays< BasisFunctionType > &trialTransformations, const CollectionOf3dArrays< KernelType > &kernels, const std::vector< CoordinateType > &quadWeights, arma::Mat< ResultType > &result) const =0
	Evaluate the integral using a non-tensor-product quadrature rule. More...

Detailed Description

template<typename BasisFunctionType_, typename KernelType_, typename ResultType_>
class Fiber::TestKernelTrialIntegral< BasisFunctionType_, KernelType_, ResultType_ >

An integral representing the weak form of an integral operator.

This class represents the integral

$\int_\Gamma \int_\Sigma I(x, y)\, d\Gamma(x)\, d\Sigma(y),$

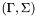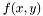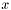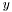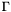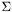defined on a pair of test and trial elements $(\Gamma, \Sigma)$ , where the integrand $f(x, y)$ may depend on any number of kernels, test and trial function transformations, and on any geometrical data related to the points $x$ and $y$ (e.g. their global coordinates or the unit vector normal to $\Gamma$ and $\Sigma$ at these points).

Template Parameters

BasisFunctionType_	Type of the values of the (components of the) basis functions occurring in the integral (possibly in a transformed form).
KernelType_	Type of the values of the (components of the) kernel functions occurring in the integral.
ResultType_	Type used to represent the value of the integral.

All three template parameters can take the following values: float, double, std::complex<float> and std::complex<double>. All types must have the same precision: for instance, mixing float with std::complex<double> is not allowed. If either BasisFunctionType_ or KernelType_ is a complex type, then ResultType_ must be set to the same type.

Member Function Documentation

template<typename BasisFunctionType_, typename KernelType_, typename ResultType_>

virtual void Fiber::TestKernelTrialIntegral< BasisFunctionType_, KernelType_, ResultType_ >::addGeometricalDependencies	(	size_t &	testGeomDeps,
		size_t &	trialGeomDeps
	)		const

pure virtual

Retrieve types of geometrical data on which the integrand of this integral depends explicitly.

An implementation of this function for a particular integral should modify the testGeomDeps and trialGeomDeps bitfields by adding to them, using the bitwise OR operation, an appropriate combination of the flags defined in the enum GeometricalDataType.

For example, an integral whose integrand depends explicitly on the global coordinates of test and trial points and on the orientation of the vector normal to the trial element at trial points should modify the arguments as follows:

testGeomDeps |= GLOBALS;

trialGeomDeps |= GLOBALS | NORMALS;

Note: It is only necessary to modify testGeomDeps and trialGeomDeps if the geometric quantities occur in the integral outside any kernels or shape function transformations. For example, it is not necessary to add NORMALS to trialGeomDeps just because a weak form contains the double-layer-potential boundary operator, which requires the normal to the trial element. It is not necessary, either, to ever add the flag INTEGRATION_ELEMENTS as integration elements (see Bempp::Geometry::getIntegrationElements() for their definition) are automatically included in the list of geometrical data required by integrals.

Implemented in Fiber::TypicalTestScalarKernelTrialIntegralBase< BasisFunctionType_, KernelType_, ResultType_ >, Fiber::TypicalTestScalarKernelTrialIntegralBase< BasisFunctionType_, BasisFunctionType_, ResultType_ >, Fiber::TypicalTestScalarKernelTrialIntegralBase< std::complex< CoordinateType_ >, CoordinateType_, std::complex< CoordinateType_ > >, and Fiber::TypicalTestScalarKernelTrialIntegralBase< CoordinateType_, std::complex< CoordinateType_ >, std::complex< CoordinateType_ > >.

template<typename BasisFunctionType_, typename KernelType_, typename ResultType_>

virtual void Fiber::TestKernelTrialIntegral< BasisFunctionType_, KernelType_, ResultType_ >::evaluateWithNontensorQuadratureRule	(	const GeometricalData< CoordinateType > &	testGeomData,
		const GeometricalData< CoordinateType > &	trialGeomData,
		const CollectionOf3dArrays< BasisFunctionType > &	testTransformations,
		const CollectionOf3dArrays< BasisFunctionType > &	trialTransformations,
		const CollectionOf3dArrays< KernelType > &	kernels,
		const std::vector< CoordinateType > &	quadWeights,
		arma::Mat< ResultType > &	result
	)		const

pure virtual

Evaluate the integral using a non-tensor-product quadrature rule.

This function should evaluate the integral using a quadrature rule of the form

$\int_\Gamma \int_\Sigma I(x, y)\, d\Gamma(x)\, d\Sigma(y) = \int_{\hat\Gamma} \int_{\hat\Sigma} I(x(\hat x), y(\hat y)) \, \mu(\hat x) \, \nu(\hat y) \, d\hat\Gamma(\hat x)\, d\hat\Sigma(\hat y) \approx \sum_{p=1}^P w_p \, I(x(\hat x_p), y(\hat y_p)) \, \mu(\hat x_p) \, \nu(\hat y_p),$

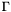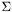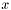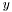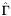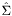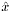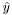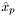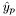where $\Gamma$ and $\Sigma$ are the test and trial elements, $x$ and $y$ the physical coordinates on these elements (global coordinates), $\hat\Gamma$ and $\hat\Sigma$ the reference test and trial elements, $\hat x$ and $\hat y$ the coordinates on the reference elements (local coordinates), $\hat x_p$ and $\hat y_p$ the local coordinates of quadrature points on the test and trial elements, 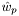$\hat w_p$ the corresponding quadrature weights, and 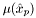$\mu(\hat x_p)$ and $\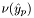nu(\hat y_p)$ the "integration elements" at the quadrature points, defined as 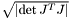$\sqrt{\lvert\det J^T J\rvert}$ , where 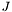$J$ is the Jacobian matrix of the local-to-global coordinate mapping.

Parameters

[in]	testGeomData	Geometrical data related to the quadrature points on the test element. The set of available geometrical data always includes integration elements.
[in]	trialGeomData	Geometrical data related to the quadrature points on the trial element. The set of available geometrical data always includes integration elements.
[in]	testTransformations	Collection of 3D arrays containing the values of test function transformations at quadrature points. The number `testTransformations[i](j, k, p)` is the jth component of the vector being the value of the ith transformation of the kth test function at the pth test quadrature point.
[in]	trialTransformations	Collection of 3D arrays containing the values of trial function transformations at quadrature points. The number `trialTransformations[i](j, k, p)` is the jth component of the vector being the value of the ith transformation of the kth trial function at the pth trial quadrature point.
[in]	kernels	Collection of 3D arrays containing the values of kernels. The number `kernels[i][(j, k, p)` is the (j, k)th entry in the tensor being the value of the ith kernel at the pth test and trial point.
[in]	testQuadWeights	Vector of the quadrature weights corresponding to the quadrature points.
[out]	result	Two-dimensional array whose (i, j)th element should contain, on output, the value of the integral involving the ith test function and jth trial function.

template<typename BasisFunctionType_, typename KernelType_, typename ResultType_>

virtual void Fiber::TestKernelTrialIntegral< BasisFunctionType_, KernelType_, ResultType_ >::evaluateWithTensorQuadratureRule	(	const GeometricalData< CoordinateType > &	testGeomData,
		const GeometricalData< CoordinateType > &	trialGeomData,
		const CollectionOf3dArrays< BasisFunctionType > &	testTransformations,
		const CollectionOf3dArrays< BasisFunctionType > &	trialTransformations,
		const CollectionOf4dArrays< KernelType > &	kernels,
		const std::vector< CoordinateType > &	testQuadWeights,
		const std::vector< CoordinateType > &	trialQuadWeights,
		arma::Mat< ResultType > &	result
	)		const

pure virtual

Evaluate the integral using a tensor-product quadrature rule.

This function should evaluate the integral using a quadrature rule of the form

$\int_\Gamma \int_\Sigma I(x, y)\, d\Gamma(x)\, d\Sigma(y) = \int_{\hat\Gamma} \int_{\hat\Sigma} I(x(\hat x), y(\hat y)) \, \mu(\hat x) \, \nu(\hat y) \, d\hat\Gamma(\hat x)\, d\hat\Sigma(\hat y) \approx \sum_{p=1}^P \sum_{q=1}^Q w_p w_q \, I(x(\hat x_p), y(\hat y_q)) \, \mu(\hat x_p) \, \nu(\hat y_q),$

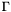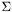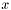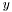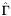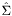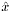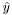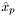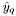where $\Gamma$ and $\Sigma$ are the test and trial elements, $x$ and $y$ the physical coordinates on these elements (global coordinates), $\hat\Gamma$ and $\hat\Sigma$ the reference test and trial elements, $\hat x$ and $\hat y$ the coordinates on the reference elements (local coordinates), $\hat x_p$ and $\hat y_q$ the local coordinates of quadrature points on the test and trial elements, 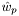$\hat w_p$ and $\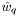hat w_q$ the corresponding quadrature weights, and 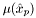$\mu(\hat x_p)$ and $\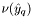nu(\hat y_q)$ the "integration elements" at the quadrature points, defined as 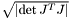$\sqrt{\lvert\det J^T J\rvert}$ , where 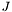$J$ is the Jacobian matrix of the local-to-global coordinate mapping.

Parameters

[in]	testGeomData	Geometrical data related to the quadrature points on the test element. The set of available geometrical data always includes integration elements.
[in]	trialGeomData	Geometrical data related to the quadrature points on the trial element. The set of available geometrical data always includes integration elements.
[in]	testTransformations	Collection of 3D arrays containing the values of test function transformations at quadrature points. The number `testTransformations[i](j, k, p)` is the jth component of the vector being the value of the ith transformation of the kth test function at the pth test quadrature point.
[in]	trialTransformations	Collection of 3D arrays containing the values of trial function transformations at quadrature points. The number `trialTransformations[i](j, k, p)` is the jth component of the vector being the value of the ith transformation of the kth trial function at the pth trial quadrature point.
[in]	kernels	Collection of 4D arrays containing the values of kernels. The number `kernels[i][(j, k, p, q)` is the (j, k)th entry in the tensor being the value of the ith kernel at the pth test point and qth trial point.
[in]	testQuadWeights	Vector of the quadrature weights corresponding to the quadrature points on the test elements.
[in]	trialQuadWeights	Vector of the quadrature weights corresponding to the quadrature points on the trial elements.
[out]	result	Two-dimensional array whose (i, j)th element should contain, on output, the value of the integral involving the ith test function and jth trial function.

The documentation for this class was generated from the following file:

/home/wojtek/Projects/BEM/bempp-sven/bempp/lib/fiber/test_kernel_trial_integral.hpp

Public Types

Public Member Functions

Detailed Description

template<typename BasisFunctionType_, typename KernelType_, typename ResultType_> class Fiber::TestKernelTrialIntegral< BasisFunctionType_, KernelType_, ResultType_ >

Member Function Documentation

template<typename BasisFunctionType_, typename KernelType_, typename ResultType_>
class Fiber::TestKernelTrialIntegral< BasisFunctionType_, KernelType_, ResultType_ >