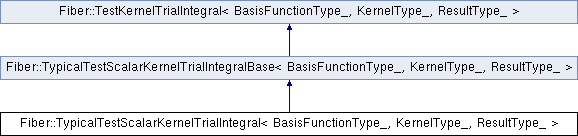
Implementation of the TestKernelTrialIntegral interface for "typical" integrals, taking advantage of BLAS during quadrature. More...

#include </home/wojtek/Projects/BEM/bempp-sven/bempp/lib/fiber/typical_test_scalar_kernel_trial_integral.hpp>

Inheritance diagram for Fiber::TypicalTestScalarKernelTrialIntegral< BasisFunctionType_, KernelType_, ResultType_ >:

Additional Inherited Members
Public Types inherited from Fiber::TypicalTestScalarKernelTrialIntegralBase< BasisFunctionType_, KernelType_, ResultType_ >
typedef Base::CoordinateType	CoordinateType

typedef Base::BasisFunctionType	BasisFunctionType

typedef Base::KernelType	KernelType

typedef Base::ResultType	ResultType

Public Types inherited from Fiber::TestKernelTrialIntegral< BasisFunctionType_, KernelType_, ResultType_ >
typedef BasisFunctionType_	BasisFunctionType

typedef KernelType_	KernelType

typedef ResultType_	ResultType

typedef ScalarTraits < ResultType >::RealType	CoordinateType

Public Member Functions inherited from Fiber::TypicalTestScalarKernelTrialIntegralBase< BasisFunctionType_, KernelType_, ResultType_ >
virtual void	addGeometricalDependencies (size_t &testGeomDeps, size_t &trialGeomDeps) const
	Retrieve types of geometrical data on which the integrand of this integral depends explicitly. More...

Public Member Functions inherited from Fiber::TestKernelTrialIntegral< BasisFunctionType_, KernelType_, ResultType_ >
virtual	~TestKernelTrialIntegral ()
	Destructor.

virtual void	evaluateWithTensorQuadratureRule (const GeometricalData< CoordinateType > &testGeomData, const GeometricalData< CoordinateType > &trialGeomData, const CollectionOf3dArrays< BasisFunctionType > &testTransformations, const CollectionOf3dArrays< BasisFunctionType > &trialTransformations, const CollectionOf4dArrays< KernelType > &kernels, const std::vector< CoordinateType > &testQuadWeights, const std::vector< CoordinateType > &trialQuadWeights, arma::Mat< ResultType > &result) const =0
	Evaluate the integral using a tensor-product quadrature rule. More...

virtual void	evaluateWithNontensorQuadratureRule (const GeometricalData< CoordinateType > &testGeomData, const GeometricalData< CoordinateType > &trialGeomData, const CollectionOf3dArrays< BasisFunctionType > &testTransformations, const CollectionOf3dArrays< BasisFunctionType > &trialTransformations, const CollectionOf3dArrays< KernelType > &kernels, const std::vector< CoordinateType > &quadWeights, arma::Mat< ResultType > &result) const =0
	Evaluate the integral using a non-tensor-product quadrature rule. More...

Detailed Description

template<typename BasisFunctionType_, typename KernelType_, typename ResultType_>
class Fiber::TypicalTestScalarKernelTrialIntegral< BasisFunctionType_, KernelType_, ResultType_ >

Implementation of the TestKernelTrialIntegral interface for "typical" integrals, taking advantage of BLAS during quadrature.

This class implements the interface defined by TestKernelTrialIntegral, assuming that the integral has the form

$\int_\Gamma \int_\Sigma \sum_{i=1}^n \vec \phi_i(x) \cdot K(x, y) \, \vec \psi_i(y) \, d\Gamma(x)\, d\Sigma(y)$

or

$\int_\Gamma \int_\Sigma \sum_{i=1}^n \vec \phi_i(x) \cdot K_i(x, y) \, \vec \psi_i(y) \, d\Gamma(x)\, d\Sigma(y)$

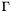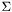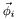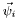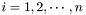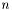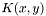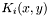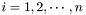where $\Gamma$ is a test element and $\Sigma$ a trial element, $\vec \phi_i$ and $\vec \psi_i$ ( $i = 1, 2, \cdots, n$ wih $n$ an integer) are test and trial function transformations, and $K(x, y)$ or $K_i(x, y)$ (( $i = 1, 2, \cdots, n$ ) are scalar kernels.

The integrals are evaluated numerically; BLAS matrix-matrix multiplication routines are used to speed up the process.

The documentation for this class was generated from the following files:

/home/wojtek/Projects/BEM/bempp-sven/bempp/lib/fiber/typical_test_scalar_kernel_trial_integral.hpp
/home/wojtek/Projects/BEM/bempp-sven/bempp/lib/fiber/typical_test_scalar_kernel_trial_integral.cpp

Additional Inherited Members

Detailed Description

template<typename BasisFunctionType_, typename KernelType_, typename ResultType_> class Fiber::TypicalTestScalarKernelTrialIntegral< BasisFunctionType_, KernelType_, ResultType_ >

template<typename BasisFunctionType_, typename KernelType_, typename ResultType_>
class Fiber::TypicalTestScalarKernelTrialIntegral< BasisFunctionType_, KernelType_, ResultType_ >