Local operators

Classes
class	Bempp::GeneralElementaryLocalOperator< BasisFunctionType_, ResultType_ >
	Standard implementation of an elementary local operator. More...
class	Bempp::IdentityOperator< BasisFunctionType_, ResultType_ >
	Identity operator. More...
class	Bempp::Maxwell3dIdentityOperator< BasisFunctionType_, ResultType_ >
	"Identity operator" for Maxwell equations in 3D. More...

Functions
template<typename BasisFunctionType , typename ResultType >
BoundaryOperator < BasisFunctionType, ResultType >	Bempp::laplaceBeltrami3dOperator (const shared_ptr< const Context< BasisFunctionType, ResultType > > &context, const shared_ptr< const Space< BasisFunctionType > > &domain, const shared_ptr< const Space< BasisFunctionType > > &range, const shared_ptr< const Space< BasisFunctionType > > &dualToRange, const std::string &label="", int symmetry=NO_SYMMETRY)
	Construct a BoundaryOperator object representing a Laplace-Beltrami operator in 3D. More...

Detailed Description

This submodule contains classes representing local operators (e.g. the identity operator) and functions used to create such operators.

Function Documentation

template<typename BasisFunctionType , typename ResultType >

BoundaryOperator< BasisFunctionType, ResultType > Bempp::laplaceBeltrami3dOperator	(	const shared_ptr< const Context< BasisFunctionType, ResultType > > &	context,
		const shared_ptr< const Space< BasisFunctionType > > &	domain,
		const shared_ptr< const Space< BasisFunctionType > > &	range,
		const shared_ptr< const Space< BasisFunctionType > > &	dualToRange,
		const std::string &	label = "",
		int	symmetry = NO_SYMMETRY
	)

Construct a BoundaryOperator object representing a Laplace-Beltrami operator in 3D.

The weak form of the Laplace-Beltrami operator 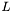in 3D is

where 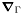is the surface gradient operator.

Parameters

[in]	context	A Context object that will be used to build the weak form of the identity operator when necessary.
[in]	domain	Function space being the domain of the identity operator.
[in]	range	Function space being the range of the identity operator.
[in]	dualToRange	Function space dual to the the range of the identity operator.
[in]	label	Textual label of the identity operator (optional, used for debugging).
[in]	symmetry	Symmetry of the weak form of the operator. Can be any combination of the flags defined in the enumeration type Symmetry.

All the three spaces must be defined on the same grid. See AbstractBoundaryOperator for the documentation of the template parameters.