Integral operator with weak form assembled from several pieces. More...

#include </home/wojtek/Projects/BEM/bempp-sven/bempp/lib/assembly/synthetic_integral_operator.hpp>

Inheritance diagram for Bempp::SyntheticIntegralOperator< BasisFunctionType_, ResultType_ >:

Public Types
typedef Base::BasisFunctionType	BasisFunctionType
	Type of the values of the (components of the) basis functions into which functions acted upon by the operator are expanded. More...

typedef Base::ResultType	ResultType
	Type used to represent elements of the weak form of the operator. More...

typedef Base::CoordinateType	CoordinateType
	Type used to represent coordinates. More...

typedef Base::QuadratureStrategy	QuadratureStrategy
	Type of the appropriate instantiation of Fiber::QuadratureStrategy. More...

typedef Fiber::LocalAssemblerForOperators < ResultType >	LocalAssembler

Public Types inherited from Bempp::AbstractBoundaryOperator< BasisFunctionType_, ResultType_ >
typedef BasisFunctionType_	BasisFunctionType
	Type of the values of the (components of the) basis functions into which functions acted upon by the operator are expanded.

typedef ResultType_	ResultType
	Type used to represent elements of the weak form of the operator.

typedef ScalarTraits < ResultType >::RealType	CoordinateType
	Type used to represent coordinates.

typedef Fiber::QuadratureStrategy < BasisFunctionType, ResultType, GeometryFactory >	QuadratureStrategy
	Type of the appropriate instantiation of Fiber::QuadratureStrategy.

Public Member Functions
	SyntheticIntegralOperator (const std::vector< BoundaryOperator< BasisFunctionType, ResultType > > &testLocalOps, const BoundaryOperator< BasisFunctionType, ResultType > &integralOp, const std::vector< BoundaryOperator< BasisFunctionType, ResultType > > &trialLocalOps, const std::string &label="", int syntheseSymmetry=NO_SYMMETRY)
	Constructor. More...

virtual bool	isLocal () const
	Return whether this operator is local. More...

Public Member Functions inherited from Bempp::AbstractBoundaryOperator< BasisFunctionType_, ResultType_ >
	AbstractBoundaryOperator (const shared_ptr< const Space< BasisFunctionType > > &domain, const shared_ptr< const Space< BasisFunctionType > > &range, const shared_ptr< const Space< BasisFunctionType > > &dualToRange, const std::string &label, int symmetry)
	Constructor. More...

virtual	~AbstractBoundaryOperator ()
	Destructor.

virtual BEMPP_DEPRECATED shared_ptr< const AbstractBoundaryOperatorId >	id () const
	Return the identifier of this operator. More...

shared_ptr< const Space < BasisFunctionType > >	domain () const
	Domain. More...

shared_ptr< const Space < BasisFunctionType > >	range () const
	Range. More...

shared_ptr< const Space < BasisFunctionType > >	dualToRange () const
	Dual to range. More...

std::string	label () const
	Return the label of the operator.

int	symmetry () const
	Return the symmetry properties of the operator. More...

shared_ptr < DiscreteBoundaryOperator < ResultType_ > >	assembleWeakForm (const Context< BasisFunctionType_, ResultType_ > &context) const
	Assemble and return the operator's weak form. More...

Static Public Member Functions
static void	getContextsForInternalAndAuxiliaryOperators (const shared_ptr< const Context< BasisFunctionType, ResultType > > &context, shared_ptr< const Context< BasisFunctionType, ResultType > > &internalContext, shared_ptr< const Context< BasisFunctionType, ResultType > > &auxContext)
	Get contexts appropriate for construction of internal integral operators and auxiliary local operators.

Static Public Member Functions inherited from Bempp::AbstractBoundaryOperator< BasisFunctionType_, ResultType_ >
static std::string	uniqueLabel ()
	Generate and return a new unique label "OpN", where N is a number.

Protected Member Functions
virtual shared_ptr < DiscreteBoundaryOperator < ResultType_ > >	assembleWeakFormImpl (const Context< BasisFunctionType, ResultType > &context) const
	Assemble and return the operator's weak form. More...

Protected Member Functions inherited from Bempp::AbstractBoundaryOperator< BasisFunctionType_, ResultType_ >
void	collectDataForAssemblerConstruction (const AssemblyOptions &options, shared_ptr< Fiber::RawGridGeometry< CoordinateType > > &testRawGeometry, shared_ptr< Fiber::RawGridGeometry< CoordinateType > > &trialRawGeometry, shared_ptr< GeometryFactory > &testGeometryFactory, shared_ptr< GeometryFactory > &trialGeometryFactory, shared_ptr< std::vector< const Fiber::Shapeset< BasisFunctionType_ > * > > &testShapesets, shared_ptr< std::vector< const Fiber::Shapeset< BasisFunctionType_ > * > > &trialShapesets, shared_ptr< Fiber::OpenClHandler > &openClHandler, bool &cacheSingularIntegrals) const
	Given an AssemblyOptions object, construct objects necessary for subsequent local assembler construction.

void	collectOptionsIndependentDataForAssemblerConstruction (shared_ptr< Fiber::RawGridGeometry< CoordinateType > > &testRawGeometry, shared_ptr< Fiber::RawGridGeometry< CoordinateType > > &trialRawGeometry, shared_ptr< GeometryFactory > &testGeometryFactory, shared_ptr< GeometryFactory > &trialGeometryFactory, shared_ptr< std::vector< const Fiber::Shapeset< BasisFunctionType_ > * > > &testShapesets, shared_ptr< std::vector< const Fiber::Shapeset< BasisFunctionType_ > * > > &trialShapesets) const
	Construct those objects necessary for subsequent local assembler construction that are independent from assembly options.

void	collectOptionsDependentDataForAssemblerConstruction (const AssemblyOptions &options, const shared_ptr< Fiber::RawGridGeometry< CoordinateType > > &testRawGeometry, const shared_ptr< Fiber::RawGridGeometry< CoordinateType > > &trialRawGeometry, shared_ptr< Fiber::OpenClHandler > &openClHandler, bool &cacheSingularIntegrals) const
	Construct those objects necessary for subsequent local assembler construction that depend on assembly options.

Private Types
typedef AbstractBoundaryOperator < BasisFunctionType_, ResultType_ >	Base

Detailed Description

template<typename BasisFunctionType_, typename ResultType_>
class Bempp::SyntheticIntegralOperator< BasisFunctionType_, ResultType_ >

Integral operator with weak form assembled from several pieces.

This class can be used to construct an integral operator assembled in the following way [1], which in ACA mode may be less time-consuming, though more memory-consuming. Suppose the formula for the 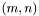$(m, n)$ th entry of the weak form of the operator in question can be written as

$A_{mn} = \sum_{\alpha} \int_\Gamma \int_\Sigma f_{\alpha m}^*(x) \, K_{\alpha}(x, y) \, g_{\alpha n}(y)\, \mathrm{d}\Gamma(x)\, \mathrm{d}\Sigma(y),$

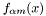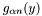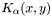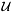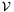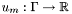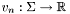where $f_{\alpha m}(x)$ and $g_{\alpha n}(y)$ are scalar-valued transformations of test and trial shape functions (e.g. basis functions, individual components of their surface curls etc.) and $K_\alpha(x, y)$ kernel functions. 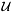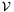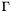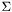Let $\mathcal U$ and $\mathcal V$ be two boundary-element spaces spanned by basis functions $u_m : \Gamma \to \mathbb{R}$ and $v_n : \Sigma \to \mathbb{R}$ such that the support of each basis function consists of a single element of the respective mesh; for example, $\mathcal U$ and $\mathcal V$ can be the spaces of piecewise constant or linear, discontinuous functions defined on $\Gamma$ and $\Sigma$ . 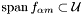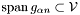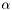Provided that $\mathrm{span}\,f_{\alpha m} \subset \mathcal U$ and $\mathrm{span}\,g_{\alpha n} \subset \mathcal V$ for all $\alpha$ , the matrix 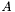$A$ can be rewritten as

$A = \sum_\alpha U_\alpha I_{\mathcal U}^{-1} K_\alpha I_{\mathcal V}^{-1} V_\alpha,$

with the entries of the individual matrices given by

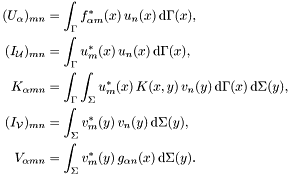
$\begin{align*} (U_{\alpha})_{mn} &= \int_\Gamma f_{\alpha m}^*(x)\,u_n(x) \,\mathrm{d}\Gamma(x),\\ (I_{\mathcal U})_{mn} &= \int_\Gamma u_m^*(x)\,u_n(x) \,\mathrm{d}\Gamma(x),\\ K_{\alpha mn} &= \int_\Gamma \int_\Sigma u_m^*(x)\,K(x,y)\,v_n(y) \,\mathrm{d}\Gamma(x)\,\mathrm{d}\Sigma(y),\\ (I_{\mathcal V})_{mn} &= \int_\Sigma v_m^*(y)\,v_n(y) \,\mathrm{d}\Sigma(y),\\ V_{\alpha mn} &= \int_\Sigma v_m^*(y)\,g_{\alpha n}(x) \,\mathrm{d}\Sigma(y). \end{align*}$

All these matrices except 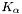$K_\alpha$ are sparse, and ACA-based assembly of 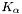$K_\alpha$ can potentially take less time than that of 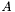$A$ because each entry of the former is an integral over a single pair of elements, while the entries of 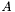$A$ may contain contributions from many element pairs.

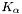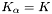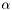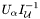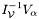In the current implementation we only handle the case of equal $K_\alpha$ , i.e. $K_\alpha = K$ for all $\alpha$ . In addition, we coalesce $U_{\alpha} I_{\mathcal U}^{-1}$ and $I_{\mathcal V}^{-1} V_{\alpha}$ into single sparse matrices.

[1] This method was proposed by Lars Kielhorn in "On single- and multi-trace implementations for scattering problems with BETL", 10. Workshop on Fast Boundary Element Methods in Industrial Applications, Soellerhaus 27-30 September 2012.

Member Typedef Documentation

template<typename BasisFunctionType_ , typename ResultType_ >

typedef Base::BasisFunctionType Bempp::SyntheticIntegralOperator< BasisFunctionType_, ResultType_ >::BasisFunctionType

Type of the values of the (components of the) basis functions into which functions acted upon by the operator are expanded.

template<typename BasisFunctionType_ , typename ResultType_ >

typedef Base::CoordinateType Bempp::SyntheticIntegralOperator< BasisFunctionType_, ResultType_ >::CoordinateType

Type used to represent coordinates.

template<typename BasisFunctionType_ , typename ResultType_ >

typedef Base::QuadratureStrategy Bempp::SyntheticIntegralOperator< BasisFunctionType_, ResultType_ >::QuadratureStrategy

Type of the appropriate instantiation of Fiber::QuadratureStrategy.

template<typename BasisFunctionType_ , typename ResultType_ >

typedef Base::ResultType Bempp::SyntheticIntegralOperator< BasisFunctionType_, ResultType_ >::ResultType

Type used to represent elements of the weak form of the operator.

Constructor & Destructor Documentation

template<typename BasisFunctionType , typename ResultType >

Bempp::SyntheticIntegralOperator< BasisFunctionType, ResultType >::SyntheticIntegralOperator	(	const std::vector< BoundaryOperator< BasisFunctionType, ResultType > > &	testLocalOps,
		const BoundaryOperator< BasisFunctionType, ResultType > &	integralOp,
		const std::vector< BoundaryOperator< BasisFunctionType, ResultType > > &	trialLocalOps,
		const std::string &	label = `""`,
		int	syntheseSymmetry = `NO_SYMMETRY`
	)

Constructor.

Parameters

[in]	testLocalOps	Vector of the operators 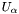$U_\alpha$ , as described above.
[in]	integralOp	The operator 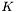, as described above.
[in]	trialLocalOps	Vector of the operators 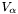$V_\alpha$ , as described above.
[in]	label	(Optional) operator label.
[in]	syntheseSymmetry	Symmetry flag (see below).

All operators passed as elements of testLocalOps and trialLocalOps must be local.

If syntheseSymmetry is equal to NO_SYMMETRY, either testLocalOps or trialLocalOps may be empty. In the former case, 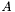$A$ is assembled as 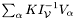$\sum_\alpha K I_{\mathcal V}^{-1} V_\alpha$ ; in the latter, as 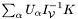$\sum_\alpha U_\alpha I_{\mathcal V}^{-1} K$ . testLocalOps and trialLocalOps must not be empty at the same time.

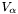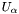If syntheseSymmetry contains the flag SYMMETRIC and/or HERMITIAN, trialLocalOps should be left empty and $V_\alpha$ are taken as the transposes or Hermitian transposes of $U_\alpha$ .

Member Function Documentation

template<typename BasisFunctionType , typename ResultType >

shared_ptr< DiscreteBoundaryOperator< ResultType > > Bempp::SyntheticIntegralOperator< BasisFunctionType, ResultType >::assembleWeakFormImpl ( const Context< BasisFunctionType, ResultType > & context ) const

protectedvirtual

Assemble and return the operator's weak form.

This virtual function is invoked by assembleWeakForm() to do the actual work.

Implements Bempp::AbstractBoundaryOperator< BasisFunctionType_, ResultType_ >.

References Bempp::Context< BasisFunctionType, ResultType >::assemblyOptions(), and Bempp::AssemblyOptions::verbosityLevel().

template<typename BasisFunctionType , typename ResultType >

bool Bempp::SyntheticIntegralOperator< BasisFunctionType, ResultType >::isLocal ( ) const

virtual

Return whether this operator is local.

Suppose that an operator 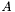$A$ acting on a function 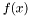$f(x)$ produces another function 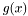$g(x)$ . We say that 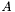$A$ is local if the value of 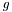$g$ at any point 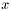$x$ depends only on the values of 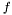$f$ in an infinitesimal neighbourhood of $x$ .

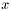Multiplicative and differential operators are local and discretization of their weak forms with finite elements leads to sparse matrices. Conversely, integral operators are in general non-local and discretization of their weak forms leads to dense matrices.

Implements Bempp::AbstractBoundaryOperator< BasisFunctionType_, ResultType_ >.

The documentation for this class was generated from the following files:

/home/wojtek/Projects/BEM/bempp-sven/bempp/lib/assembly/synthetic_integral_operator.hpp
/home/wojtek/Projects/BEM/bempp-sven/bempp/lib/assembly/synthetic_integral_operator.cpp

Public Types

Public Member Functions

Static Public Member Functions

Protected Member Functions

Private Types

Detailed Description

template<typename BasisFunctionType_, typename ResultType_> class Bempp::SyntheticIntegralOperator< BasisFunctionType_, ResultType_ >

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

template<typename BasisFunctionType_, typename ResultType_>
class Bempp::SyntheticIntegralOperator< BasisFunctionType_, ResultType_ >