Fast assembly via Hierarchical matrices¶
Assembling boundary integral operators is expensive since the matrices are generally dense. Hence, if \(N\) is the number of elements in the grid the overall complexity of the assembly grows like \(O(N^3)\) and the cost of a matrix-vector product grows like \(O(N^2)\). This makes large problems infeasible on standard hardware.
In recent years two techniques have been established to speed-up the assembly of boundary integral operators: Fast Multipole Methods (FMM) and Hierarchical Matrix (H-Matrix) techniques. BEM++ currently implements the latter one. It brings down the cost of assembly and matrix-vector products for integral operators to \(O(N\log N)\), making even larger problems with hundred thousands of degrees of freedom possible on a single workstation.
Introduction to hierarchical matrices¶
Hierarchical matrices are a complex topic. For a good introduction we refer to the MPI Lecture Notes on hierarchical matrices. Another good resource is the recent book on hierarchical matrices by W. Hackbusch.
Using hierarchical matrix assembly¶
Fast H-Matrix assembly of boundary and potential operators is enabled
by default in BEM++. The corresponding options are
bempp.api.global_parameters.assembly.boundary_operator_assembly_type
and bempp.api.global_parameters.assembly.potential_operator_assembly_type.
By default both are set to \(hmat\), which enables H-Matrix assembly.
For very small problems it is advisable to change the boundary operator
assembly type to dense as there is a larger overhead of H-Matrix
techniques for small problems.
A range of parameters controls the H-Matrix assembly itself. The most
important one is the accuracy parameter bempp.api.global_parameters.hmat.eps.
This specifies the accuracy of the H-Matrix approximation, and by default is
set to \(1E-3\). The best value is problem dependent. In the following we
summarize all parameters that control the assembly. For very large problems
it is also advisable to inrease the value of bempp.api.global_parameters.hmat.max_block_size.
As default it is set to \(2048\). This restricts the largest size an admissible matrix
block can have that will be low-rank approximated. Choosing a very large value can
have negative effect on the load-balancing between the different cores during assembly.
Choosing a too small value can lead to a significant increase in overall computational
complexity.
By default BEM++ uses a coarsening strategy to post-process the hierarchical matrix
assembly und further reduce the amount of memory an H-Matrix requires. This post-processing
is based an randomized low-rank approximations. In most of our experiments it increased
the assembly time by around 10% and often reduced the memory consumption by close to
50%. However, if it is not desired then the parameter
bempp.api.global_parameters.hmat.coarsening should be set to False. The accuracy
of the coarsening strategy is by default the same as the assembly. Other values can be
set by modifying bempp.api.global_parameters.hmat.coarsening_accuracy.
Querying hierarchical matrices¶
Operators assembled via hierarchical matrices mostly behave in the same way as operators
assembled using dense matrix techniques and the interface is identical. However, it is often
desirable to query advanced information from H-Matrices. This is implemented in the
module bempp.api.hmatrix_interface.
Let us assemble a simple H-Matrix operator over a regular sphere.
import bempp.api
grid = bempp.api.shapes.regular_sphere(4)
space = bempp.api.function_space(grid, "DP", 0)
discrete_operator = bempp.api.operators.boundary.laplace.single_layer(
space, space, space).weak_form()
Since H-Matrix assemble is automatically active we do not have to do anything else. We can now collect some information on the H-Matrix.
To find out the memory consumption in kb we can use
bempp.api.hmatrix_interface.mem_size(discrete_operator)
This will show the amount of storage that the H-Matrix data needs (not that it does not count storage of administrational data such as the underlying tree structure).
The total number of blocks in the H-Matrix is given by
bempp.api.hmatrix_interface.number_of_blocks(discrete_operator)
Similar commands exist for the number of dense blocks and the number of low-rank blocks.
BEM++ also gives access to the complete underlying tree structure. To obtain the block cluster tree the command
tree = bempp.api.hmatrix_interface.block_cluster_tree(discrete_operator)
can be used. To plot the tree call
tree.plot()
This command requires that PyQt4 is installed.
An iterator over all leaf nodes of the tree is given by tree.leaf_nodes. The root node
of the tree is obtained by
root = tree.root
From the root node the tree can be traversed hierarchically. The children of a node are available through an iterator. Hence, to iterate through the four children of root use
for child in root.children:
print((child.row_cluster_range, child.column_cluster_range))
This prints out the ranges of the four subnodes of root. Subnodes are traversed
in C-style order. Hence, if at the first level the H-Matrix has the form
the children iterator returns the nodes in the order \(A_{11}\), \(A_{12}\),
\(A_{21}\), \(A_{22}\).
To get from the leafs of the block cluster tree to the data associated with the leafs the function
bempp.api.hmatrix_interface.data_block can be used.
For example, the following code makes a histogram plot of the ranks of the data for all admissible nodes in the above created H-Matrix.
import matplotlib.pyplot as plt
admissible_nodes = [node for node in tree.leaf_nodes if node.admissible]
ranks = [bempp.api.hmatrix_interface.data_block(discrete_operator, node).rank \
for node in admissible_nodes]
plt.hist(ranks)
plt.xlabel('Rank')
plt.ylabel('Number of blocks')
plt.show()
The result looks as follows.
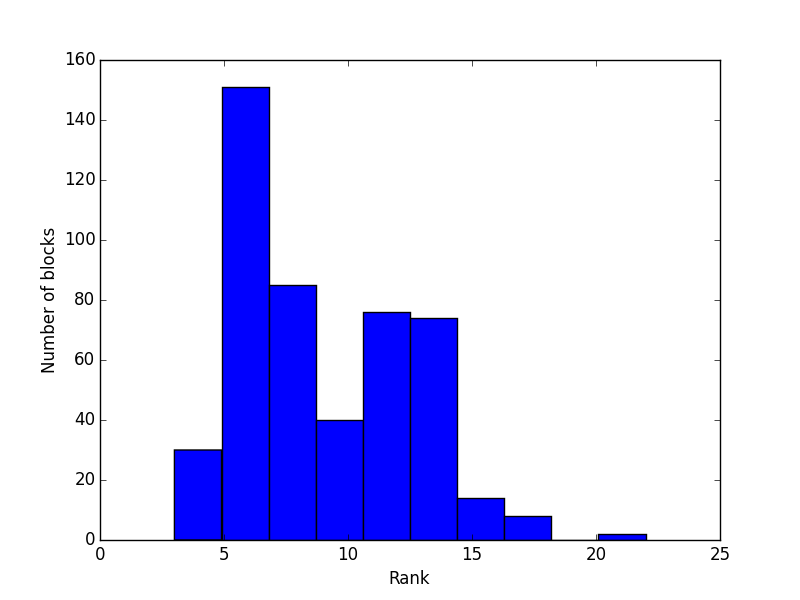
Most low-rank data blocks are compressed down to a rank of around six.
Function and class reference¶
-
class
bempp.core.hmat.block_cluster_tree.BlockClusterTree¶ Interface to the block cluster tree structre of an H-Matrix.
-
leaf_nodes¶ Return an iterator over the leaf nodes.
-
plot(self, file_name='block_cluster_tree.png', display=True, width=2000, height=2000, delete=True)¶ Plot a given block cluster tree into a file. If display is True the plot is also displayed.
Parameters: - file_name (string) – name of the output file.
- display (bool) – If True also display the plot.
- width (int) – Width in pixels.
- height (int) – Height in pixels.
- delete (bool) – If True image is deleted after displaying it.
Notes
This method requires that PyQt4 is installed.
-
root¶ Return the root node of the tree.
-
-
class
bempp.core.hmat.block_cluster_tree.BlockClusterTreeNode¶ Interface to a single node of the block cluster tree.
-
admissible¶ Return True if the node is admissible, otherwise False.
-
child(self, int i)¶ Access to a child node by index 0 <= i < 4.
-
children¶ Return an iterator over all child nodes.
-
cluster_distance¶ Return the distance between the associated row and column cluster node.
-
column_cluster_range¶ Return the range of the associated column cluster node.
-
diameters¶ Return a tuple with the diameters of the row cluster bounding box and the column cluster bounding box.
-
is_leaf¶ Return True if the node is a leaf, otherwise False.
-
row_cluster_range¶ Return the range of the associated row cluster node.
-
shape¶ Return the shape of the block represented by this node.
-
-
class
bempp.core.hmat.hmatrix_data.HMatrixDataBase¶ Base class for H-Matrix data.
-
block_type¶ Returns the type of the data block (dense or low_rank_ab).
-
dtype¶ Returns the data type.
-
mem_size¶ Returns the memory size in kb of the data.
-
rank¶ Returns the rank of the data.
-
shape¶ Returns the shape of the data block.
-
-
class
bempp.core.hmat.hmatrix_data.HMatrixLowRankData¶ Interface to low-rank H-Matrix data.
This class provides an interface to low-rank H-Matrix data. Algebraically, the stored matrix D has the form D = A * B, where A is an (m, k) matrix and B a (k, n) matrix. Here, k is the rank, m is the number of rows and n is the number of columns.
-
A¶ Returns the matrix A as NumPy array.
-
B¶ Returns the matrix B as NumPy array.
-
-
class
bempp.core.hmat.hmatrix_data.HMatrixDenseData¶ Interface to dense H-Matrix data.
This class provides an interface to dense H-Matrix data, that is internally the data is stored as a dense matrix A.
-
A¶ Return the dense matrix.
-
-
bempp.api.hmat.hmatrix_interface.number_of_blocks(discrete_operator)¶ Return the number of blocks for a HMatrix operator.
-
bempp.api.hmat.hmatrix_interface.number_of_dense_blocks(discrete_operator)¶ Return the number of dense blocks for a HMatrix operator.
-
bempp.api.hmat.hmatrix_interface.number_of_low_rank_blocks(discrete_operator)¶ Return the number of low rank blocks for a HMatrix operator.
-
bempp.api.hmat.hmatrix_interface.mem_size(discrete_operator)¶ Return the memory size in kb for a HMatrix operator.
-
bempp.api.hmat.hmatrix_interface.block_cluster_tree(discrete_operator)¶ Return the block cluster tree for a HMatrix operator.
-
bempp.api.hmat.hmatrix_interface.data_block(discrete_operator, block_cluster_tree_node)¶ Return the data block associated with a block cluster tree node.