|
BEM++
2.0
|
|
BEM++
2.0
|
Numerical quadrature strategy. More...
#include </home/wojtek/Projects/BEM/bempp-sven/bempp/lib/assembly/numerical_quadrature_strategy.hpp>

Public Types | |
| typedef Base::CoordinateType | CoordinateType |
 Public Types inherited from Fiber::NumericalQuadratureStrategy< BasisFunctionType, ResultType, GeometryFactory > Public Types inherited from Fiber::NumericalQuadratureStrategy< BasisFunctionType, ResultType, GeometryFactory > | |
| typedef Base::CoordinateType | CoordinateType |
 Public Types inherited from Fiber::NumericalQuadratureStrategyBase< BasisFunctionType, ResultType, GeometryFactory, void > Public Types inherited from Fiber::NumericalQuadratureStrategyBase< BasisFunctionType, ResultType, GeometryFactory, void > | |
|
typedef QuadratureStrategy < BasisFunctionType, ResultType, GeometryFactory, void > | Base |
| typedef Base::CoordinateType | CoordinateType |
 Public Types inherited from Fiber::QuadratureStrategy< BasisFunctionType, ResultType, GeometryFactory, void > Public Types inherited from Fiber::QuadratureStrategy< BasisFunctionType, ResultType, GeometryFactory, void > | |
| typedef Base::CoordinateType | CoordinateType |
 Public Types inherited from Fiber::QuadratureStrategyBase< BasisFunctionType, ResultType, GeometryFactory > Public Types inherited from Fiber::QuadratureStrategyBase< BasisFunctionType, ResultType, GeometryFactory > | |
|
typedef ScalarTraits < ResultType >::RealType | CoordinateType |
Public Member Functions | |
| NumericalQuadratureStrategy () | |
| Construct a numerical quadrature strategy with default accuracy settings. More... | |
| NumericalQuadratureStrategy (const AccuracyOptionsEx &accuracyOptions) | |
| Construct a numerical quadrature strategy with prescribed accuracy settings. More... | |
| NumericalQuadratureStrategy (const AccuracyOptionsEx &accuracyOptions, const shared_ptr< const SingleQuadratureRuleFamily< CoordinateType > > &singleQuadratureRuleFamily, const shared_ptr< const DoubleQuadratureRuleFamily< CoordinateType > > &doubleQuadratureRuleFamily) | |
| Construct a numerical quadrature strategy. More... | |
| NumericalQuadratureStrategy (const shared_ptr< const QuadratureDescriptorSelectorFactory< BasisFunctionType > > &quadratureDescriptorSelectorFactory, const shared_ptr< const SingleQuadratureRuleFamily< CoordinateType > > &singleQuadratureRuleFamily, const shared_ptr< const DoubleQuadratureRuleFamily< CoordinateType > > &doubleQuadratureRuleFamily) | |
| Construct a numerical quadrature strategy. More... | |
 Public Member Functions inherited from Fiber::NumericalQuadratureStrategy< BasisFunctionType, ResultType, GeometryFactory > Public Member Functions inherited from Fiber::NumericalQuadratureStrategy< BasisFunctionType, ResultType, GeometryFactory > | |
| NumericalQuadratureStrategy () | |
| Construct a numerical quadrature strategy. More... | |
| NumericalQuadratureStrategy (const AccuracyOptionsEx &accuracyOptions) | |
| Construct a numerical quadrature strategy. More... | |
| NumericalQuadratureStrategy (const AccuracyOptionsEx &accuracyOptions, const shared_ptr< const SingleQuadratureRuleFamily< CoordinateType > > &singleQuadratureRuleFamily, const shared_ptr< const DoubleQuadratureRuleFamily< CoordinateType > > &doubleQuadratureRuleFamily) | |
| Construct a numerical quadrature strategy. More... | |
| NumericalQuadratureStrategy (const shared_ptr< const QuadratureDescriptorSelectorFactory< BasisFunctionType > > &quadratureDescriptorSelectorFactory, const shared_ptr< const SingleQuadratureRuleFamily< CoordinateType > > &singleQuadratureRuleFamily, const shared_ptr< const DoubleQuadratureRuleFamily< CoordinateType > > &doubleQuadratureRuleFamily) | |
| Construct a numerical quadrature strategy. More... | |
 Public Member Functions inherited from Fiber::NumericalQuadratureStrategyBase< BasisFunctionType, ResultType, GeometryFactory, void > Public Member Functions inherited from Fiber::NumericalQuadratureStrategyBase< BasisFunctionType, ResultType, GeometryFactory, void > | |
| NumericalQuadratureStrategyBase (const shared_ptr< const QuadratureDescriptorSelectorFactory< BasisFunctionType > > &quadratureDescriptorSelectorFactory, const shared_ptr< const SingleQuadratureRuleFamily< CoordinateType > > &singleQuadratureRuleFamily, const shared_ptr< const DoubleQuadratureRuleFamily< CoordinateType > > &doubleQuadratureRuleFamily) | |
| virtual std::auto_ptr < LocalAssemblerForLocalOperators < ResultType > > | makeAssemblerForIdentityOperators (const shared_ptr< const GeometryFactory > &geometryFactory, const shared_ptr< const RawGridGeometry< CoordinateType > > &rawGeometry, const shared_ptr< const std::vector< const Shapeset< BasisFunctionType > * > > &testShapesets, const shared_ptr< const std::vector< const Shapeset< BasisFunctionType > * > > &trialShapesets, const shared_ptr< const CollectionOfShapesetTransformations< CoordinateType > > &testTransformations, const shared_ptr< const CollectionOfShapesetTransformations< CoordinateType > > &trialTransformations, const shared_ptr< const OpenClHandler > &openClHandler) const |
| Allocate a Galerkin-mode local assembler for the identity operator. More... | |
|
virtual std::auto_ptr < LocalAssemblerForLocalOperators < ResultType > > | makeAssemblerForLocalOperators (const shared_ptr< const GeometryFactory > &geometryFactory, const shared_ptr< const RawGridGeometry< CoordinateType > > &rawGeometry, const shared_ptr< const std::vector< const Shapeset< BasisFunctionType > * > > &testShapesets, const shared_ptr< const std::vector< const Shapeset< BasisFunctionType > * > > &trialShapesets, const shared_ptr< const CollectionOfShapesetTransformations< CoordinateType > > &testTransformations, const shared_ptr< const CollectionOfShapesetTransformations< CoordinateType > > &trialTransformations, const shared_ptr< const TestTrialIntegral< BasisFunctionType, ResultType > > &integral, const shared_ptr< const OpenClHandler > &openClHandler) const |
| Allocate a Galerkin-mode local assembler for a local operator. | |
 Public Member Functions inherited from Fiber::QuadratureStrategy< BasisFunctionType, ResultType, GeometryFactory, void > Public Member Functions inherited from Fiber::QuadratureStrategy< BasisFunctionType, ResultType, GeometryFactory, void > | |
|
std::auto_ptr < LocalAssemblerForIntegralOperators < ResultType > > | makeAssemblerForIntegralOperators (const shared_ptr< const GeometryFactory > &testGeometryFactory, const shared_ptr< const GeometryFactory > &trialGeometryFactory, const shared_ptr< const RawGridGeometry< CoordinateType > > &testRawGeometry, const shared_ptr< const RawGridGeometry< CoordinateType > > &trialRawGeometry, const shared_ptr< const std::vector< const Shapeset< BasisFunctionType > * > > &testShapesets, const shared_ptr< const std::vector< const Shapeset< BasisFunctionType > * > > &trialShapesets, const shared_ptr< const CollectionOfShapesetTransformations< CoordinateType > > &testTransformations, const shared_ptr< const CollectionOfKernels< ResultType > > &kernels, const shared_ptr< const CollectionOfShapesetTransformations< CoordinateType > > &trialTransformations, const shared_ptr< const TestKernelTrialIntegral< BasisFunctionType, ResultType, ResultType > > &integral, const shared_ptr< const OpenClHandler > &openClHandler, const ParallelizationOptions ¶llelizationOptions, VerbosityLevel::Level verbosityLevel, bool cacheSingularIntegrals) const |
| Allocate a Galerkin-mode local assembler for an integral operator with complex kernel. | |
|
std::auto_ptr < LocalAssemblerForGridFunctions < ResultType > > | makeAssemblerForGridFunctions (const shared_ptr< const GeometryFactory > &geometryFactory, const shared_ptr< const RawGridGeometry< CoordinateType > > &rawGeometry, const shared_ptr< const std::vector< const Shapeset< BasisFunctionType > * > > &testShapesets, const shared_ptr< const CollectionOfShapesetTransformations< CoordinateType > > &testTransformations, const shared_ptr< const Function< ResultType > > &function, const shared_ptr< const OpenClHandler > &openClHandler) const |
| Allocate a local assembler for calculations of the projections of complex-valued functions from a given space on a Fiber::Function. | |
|
std::auto_ptr < EvaluatorForIntegralOperators < ResultType > > | makeEvaluatorForIntegralOperators (const shared_ptr< const GeometryFactory > &geometryFactory, const shared_ptr< const RawGridGeometry< CoordinateType > > &rawGeometry, const shared_ptr< const std::vector< const Shapeset< BasisFunctionType > * > > &trialShapesets, const shared_ptr< const CollectionOfKernels< ResultType > > &kernel, const shared_ptr< const CollectionOfShapesetTransformations< CoordinateType > > &trialTransformations, const shared_ptr< const KernelTrialIntegral< BasisFunctionType, ResultType, ResultType > > &integral, const shared_ptr< const std::vector< std::vector< ResultType > > > &argumentLocalCoefficients, const shared_ptr< const OpenClHandler > &openClHandler, const ParallelizationOptions ¶llelizationOptions) const |
| Allocate an evaluator for an integral operator with complex-valued kernel applied to a grid function. | |
|
std::auto_ptr < LocalAssemblerForPotentialOperators < ResultType > > | makeAssemblerForPotentialOperators (const arma::Mat< CoordinateType > &evaluationPoints, const shared_ptr< const GeometryFactory > &geometryFactory, const shared_ptr< const RawGridGeometry< CoordinateType > > &rawGeometry, const shared_ptr< const std::vector< const Shapeset< BasisFunctionType > * > > &trialShapesets, const shared_ptr< const CollectionOfKernels< ResultType > > &kernels, const shared_ptr< const CollectionOfShapesetTransformations< CoordinateType > > &trialTransformations, const shared_ptr< const KernelTrialIntegral< BasisFunctionType, ResultType, ResultType > > &integral, const shared_ptr< const OpenClHandler > &openClHandler, const ParallelizationOptions ¶llelizationOptions, VerbosityLevel::Level verbosityLevel) const |
| Allocate a local assembler for a potential operator with complex kernel. | |
 Public Member Functions inherited from Fiber::QuadratureStrategyBase< BasisFunctionType, ResultType, GeometryFactory > Public Member Functions inherited from Fiber::QuadratureStrategyBase< BasisFunctionType, ResultType, GeometryFactory > | |
|
std::auto_ptr < LocalAssemblerForIntegralOperators < ResultType > > | makeAssemblerForIntegralOperators (const shared_ptr< const GeometryFactory > &testGeometryFactory, const shared_ptr< const GeometryFactory > &trialGeometryFactory, const shared_ptr< const RawGridGeometry< CoordinateType > > &testRawGeometry, const shared_ptr< const RawGridGeometry< CoordinateType > > &trialRawGeometry, const shared_ptr< const std::vector< const Shapeset< BasisFunctionType > * > > &testShapesets, const shared_ptr< const std::vector< const Shapeset< BasisFunctionType > * > > &trialShapesets, const shared_ptr< const CollectionOfShapesetTransformations< CoordinateType > > &testTransformations, const shared_ptr< const CollectionOfKernels< CoordinateType > > &kernels, const shared_ptr< const CollectionOfShapesetTransformations< CoordinateType > > &trialTransformations, const shared_ptr< const TestKernelTrialIntegral< BasisFunctionType, CoordinateType, ResultType > > &integral, const shared_ptr< const OpenClHandler > &openClHandler, const ParallelizationOptions ¶llelizationOptions, VerbosityLevel::Level verbosityLevel, bool cacheSingularIntegrals) const |
| Allocate a Galerkin-mode local assembler for an integral operator with real kernel. | |
|
std::auto_ptr < LocalAssemblerForGridFunctions < ResultType > > | makeAssemblerForGridFunctions (const shared_ptr< const GeometryFactory > &geometryFactory, const shared_ptr< const RawGridGeometry< CoordinateType > > &rawGeometry, const shared_ptr< const std::vector< const Shapeset< BasisFunctionType > * > > &testShapesets, const shared_ptr< const CollectionOfShapesetTransformations< CoordinateType > > &testTransformations, const shared_ptr< const Function< ResultType > > &function, const shared_ptr< const OpenClHandler > &openClHandler) const |
| Allocate a local assembler for calculations of the projections of functions from a given space on a Fiber::Function. | |
|
std::auto_ptr < EvaluatorForIntegralOperators < ResultType > > | makeEvaluatorForIntegralOperators (const shared_ptr< const GeometryFactory > &geometryFactory, const shared_ptr< const RawGridGeometry< CoordinateType > > &rawGeometry, const shared_ptr< const std::vector< const Shapeset< BasisFunctionType > * > > &trialShapesets, const shared_ptr< const CollectionOfKernels< CoordinateType > > &kernels, const shared_ptr< const CollectionOfShapesetTransformations< CoordinateType > > &trialTransformations, const shared_ptr< const KernelTrialIntegral< BasisFunctionType, CoordinateType, ResultType > > &integral, const shared_ptr< const std::vector< std::vector< ResultType > > > &argumentLocalCoefficients, const shared_ptr< const OpenClHandler > &openClHandler, const ParallelizationOptions ¶llelizationOptions) const |
| Allocate an evaluator for an integral operator with real kernel applied to a grid function. | |
|
std::auto_ptr < LocalAssemblerForPotentialOperators < ResultType > > | makeAssemblerForPotentialOperators (const arma::Mat< CoordinateType > &evaluationPoints, const shared_ptr< const GeometryFactory > &geometryFactory, const shared_ptr< const RawGridGeometry< CoordinateType > > &rawGeometry, const shared_ptr< const std::vector< const Shapeset< BasisFunctionType > * > > &trialShapesets, const shared_ptr< const CollectionOfKernels< CoordinateType > > &kernels, const shared_ptr< const CollectionOfShapesetTransformations< CoordinateType > > &trialTransformations, const shared_ptr< const KernelTrialIntegral< BasisFunctionType, CoordinateType, ResultType > > &integral, const shared_ptr< const OpenClHandler > &openClHandler, const ParallelizationOptions ¶llelizationOptions, VerbosityLevel::Level verbosityLevel) const |
| Allocate a local assembler for a potential operator with real kernel. | |
Private Types | |
|
typedef Fiber::NumericalQuadratureStrategy < BasisFunctionType, ResultType, GeometryFactory > | Base |
Additional Inherited Members | |
 Protected Member Functions inherited from Fiber::NumericalQuadratureStrategyBase< BasisFunctionType, ResultType, GeometryFactory, void > Protected Member Functions inherited from Fiber::NumericalQuadratureStrategyBase< BasisFunctionType, ResultType, GeometryFactory, void > | |
|
shared_ptr< const QuadratureDescriptorSelectorFactory < BasisFunctionType > > | quadratureDescriptorSelectorFactory () const |
|
shared_ptr< const SingleQuadratureRuleFamily < CoordinateType > > | singleQuadratureRuleFamily () const |
|
shared_ptr< const DoubleQuadratureRuleFamily < CoordinateType > > | doubleQuadratureRuleFamily () const |
Numerical quadrature strategy.
A quadrature strategy provides functions constructing local assemblers used to discretize boundary operators and user-defined functions. A particular quadrature strategy determines how the integrals involved in this discretization are evaluated.
This is the default quadrature strategy available in BEM++. In this quadrature strategy integrals are evaluated by numerical quadrature.
The process of selecting a quadrature rule for the evaluation of a particular integral can be customized at different levels of generality. The choice of quadrature rule is done in two steps:
By default, NumericalQuadratureStrategy uses quadrature descriptor selectors being instances of the classes DefaultQuadratureDescriptorSelectorForIntegralOperators, DefaultQuadratureDescriptorSelectorForLocalOperators and DefaultQuadratureDescriptorSelectorForGridFunctions. You can make it use different selectors by passing a custom QuadratureDescriptorSelectorFactory object to the constructor of NumericalQuadratureStrategy.
The default quadrature descriptor selectors are customizable: you can control the choice of quadrature orders using an AccuracyOptionsEx options passed to another constructor of NumericalQuadratureStrategy. The documentation of this constructor gives detailed information about how AccuracyOptionsEx influences the quadrature orders.
By default, NumericalQuadratureStrategy uses the quadrature rule families being instances of DefaultDoubleQuadratureRuleFamily and DefaultSingleQuadratureRuleFamily. These use Gaussian quadrature for regular integrals and the Sauter-Schwab quadrature rules (*) for singular integrals. If you wish, you can subclass DoubleQuadratureRuleFamily and/or SingleQuadratureRuleFamily and pass their instances to a NumericalQuadratureStrategy contructor.
(*) S. Sauter, Ch. Schwab, "Boundary Element Methods" (2010).
| Bempp::NumericalQuadratureStrategy< BasisFunctionType, ResultType >::NumericalQuadratureStrategy | ( | ) |
Construct a numerical quadrature strategy with default accuracy settings.
This constructor makes the newly created object use the default quadrature descriptor selector factory and the default accuracy options.
|
explicit |
Construct a numerical quadrature strategy with prescribed accuracy settings.
This constructor makes the newly created object use the default quadrature descriptor selector factory with custom accuracy options and the default quadrature rule families.
The quadrature order is determined differently for different types of integrals:
Double integrals of the form
![\[ \int_{\Gamma} \int_{\Sigma} f(x, y) \, d\Gamma(x) \, d\Sigma(y), \]](form_122.png)
where 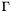 and
and 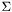 are two disjoint elements and
are two disjoint elements and 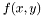 is a function regular for
is a function regular for  and
and 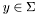 . Such integrals are approximated by
. Such integrals are approximated by
![\[ \sum_{i=1}^m \sum_{j=1}^n w_i^m w_j^n \, f(x_i^m, y_j^n), \]](form_127.png)
where  and
and  are appropriate quadrature points and
are appropriate quadrature points and 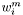 and
and  are the corresponding quadrature weights. By default, these are chosen so that the order of accuracy of the quadrature of each element is equal to the maximum degree of the polynomials belonging to the shapeset attached to that element. In other words, the quadrature rule is chosen so that a function
are the corresponding quadrature weights. By default, these are chosen so that the order of accuracy of the quadrature of each element is equal to the maximum degree of the polynomials belonging to the shapeset attached to that element. In other words, the quadrature rule is chosen so that a function 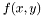 being a product of two polynomials,
being a product of two polynomials,  and
and  , with degrees equal to the orders of the shapesets attached to elements
, with degrees equal to the orders of the shapesets attached to elements 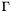 and
and 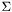 would be integrated exactly. For instance, for a pair of elements endowed with linear shapesets, single-point quadrature is by default used on both elements.
would be integrated exactly. For instance, for a pair of elements endowed with linear shapesets, single-point quadrature is by default used on both elements.
This default integration order is often insufficient. It can be increased by calling one of the overloads of the AccuracyOptionsEx::setDoubleRegular() function on the object passed subsequently to this constructor via the accuracyOptions parameter. The quadrature rule can be made dependent on the distance between the two elements; see the documentation of AccuracyOptionsEx for details.
Double integrals of the same form as above, but on pairs of elements 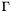 and
and 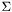 sharing at least a single point and with the function
sharing at least a single point and with the function 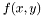 having a singularity at
having a singularity at 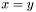 . Such integrals are evaluated by first applying an appropriate coordinate transformation to remove the singularity of the integrand, as described in the book of Sauter and Schwab cited before, and then approximating the new integral with a tensor-product Gaussian quadrature rule with order of accuracy in each dimension choosen by default as
. Such integrals are evaluated by first applying an appropriate coordinate transformation to remove the singularity of the integrand, as described in the book of Sauter and Schwab cited before, and then approximating the new integral with a tensor-product Gaussian quadrature rule with order of accuracy in each dimension choosen by default as  , where
, where  and
and  are the orders of the shapesets attached to elements
are the orders of the shapesets attached to elements 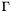 and
and 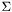 . The order of accuracy can be customized by calling the AccuracyOptionsEx::setDoubleSingular() function.
. The order of accuracy can be customized by calling the AccuracyOptionsEx::setDoubleSingular() function.
![\[ \int_{\Gamma} f(x) \, d\Gamma(x) \]](form_138.png)
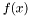 . They are evaluated using a Gaussian quadrature rule with order of accuracy taken by default as twice the order of the shapeset attached to the element
. They are evaluated using a Gaussian quadrature rule with order of accuracy taken by default as twice the order of the shapeset attached to the element 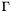 . This order of accuracy can be customized by calling the AccuracyOptionsEx::setSingleRegular() function.
. This order of accuracy can be customized by calling the AccuracyOptionsEx::setSingleRegular() function. | Bempp::NumericalQuadratureStrategy< BasisFunctionType, ResultType >::NumericalQuadratureStrategy | ( | const AccuracyOptionsEx & | accuracyOptions, |
| const shared_ptr< const SingleQuadratureRuleFamily< CoordinateType > > & | singleQuadratureRuleFamily, | ||
| const shared_ptr< const DoubleQuadratureRuleFamily< CoordinateType > > & | doubleQuadratureRuleFamily | ||
| ) |
Construct a numerical quadrature strategy.
This constructor makes the newly created object use the default quadrature descriptor selector factory with custom accuracy options and custom quadrature rule families.
| Bempp::NumericalQuadratureStrategy< BasisFunctionType, ResultType >::NumericalQuadratureStrategy | ( | const shared_ptr< const QuadratureDescriptorSelectorFactory< BasisFunctionType > > & | quadratureDescriptorSelectorFactory, |
| const shared_ptr< const SingleQuadratureRuleFamily< CoordinateType > > & | singleQuadratureRuleFamily, | ||
| const shared_ptr< const DoubleQuadratureRuleFamily< CoordinateType > > & | doubleQuadratureRuleFamily | ||
| ) |
Construct a numerical quadrature strategy.
This constructor makes the newly created object use a custom quadrature descriptor selector factory and quadrature rule families.
 1.8.5
1.8.5