|
BEM++
2.0
|
|
BEM++
2.0
|
Adaptive cross approximation (ACA) parameters. More...
#include </home/wojtek/Projects/BEM/bempp-sven/bempp/lib/assembly/aca_options.hpp>
Public Types | |
| enum | AcaAssemblyMode { MIN_ASSEMBLY_MODE, GLOBAL_ASSEMBLY = MIN_ASSEMBLY_MODE, LOCAL_ASSEMBLY, HYBRID_ASSEMBLY, MAX_ASSEMBLY_MODE = HYBRID_ASSEMBLY } |
ACA assembly mode. See documentation of the member mode for more information. | |
| enum | ReactionToUnsupportedMode { MIN_REACTION, IGNORE = MIN_REACTION, WARNING, ERROR, MAX_REACTION = ERROR } |
| Actions to take when an unsupported assembly mode is detected. More... | |
Public Member Functions | |
| AcaOptions () | |
| Initialize ACA parameters to default values. | |
Public Attributes | |
| double | eps |
| Estimate of the desired approximation accuracy. More... | |
| double | eta |
| Cluster-pair admissibility parameter. More... | |
| unsigned int | minimumBlockSize |
| Minimum size of blocks approximated with ACA. More... | |
| unsigned int | maximumBlockSize |
| Maximum allowed block size. More... | |
| unsigned int | maximumRank |
| Maximum rank of blocks stored in the low-rank format. More... | |
| AcaAssemblyMode | mode |
| ACA assembly mode. More... | |
| ReactionToUnsupportedMode | reactionToUnsupportedMode |
| Action to take when an unsupported assembly mode is detected. More... | |
| bool | recompress |
| Recompress ACA matrix after construction? More... | |
| bool | outputPostscript |
| If true, hierarchical matrix structure will be written in PostScript format at the end of the assembly procedure. More... | |
| std::string | outputFname |
| Name of the output PostScript file. More... | |
| double | scaling |
| Estimate of the magnitude of typical entries of the matrix to be approximated. More... | |
| bool | useAhmedAca |
| Choice of ACA variant. More... | |
| int | firstClusterIndex |
| Index of the first block cluster to be approximated using ACA. More... | |
| bool | globalAssemblyBeforeCompression |
| Do global assembly before ACA? More... | |
Adaptive cross approximation (ACA) parameters.
Actions to take when an unsupported assembly mode is detected.
| double Bempp::AcaOptions::eps |
Estimate of the desired approximation accuracy.
Default value: 1e-4.
| double Bempp::AcaOptions::eta |
Cluster-pair admissibility parameter.
Default value: 1.2.
| int Bempp::AcaOptions::firstClusterIndex |
Index of the first block cluster to be approximated using ACA.
This parameter is included to facilitate debugging of ACA algorithms. If it is set to a nonnegative value, ACA will process block cluster with index firstClusterIndex first.
Default value: -1 (meaning that this parameter is ignored).
| bool Bempp::AcaOptions::globalAssemblyBeforeCompression |
Do global assembly before ACA?
mode parameter to LOCAL_ASSEMBLY. Referenced by Bempp::AssemblyOptions::switchToAcaMode().
| unsigned int Bempp::AcaOptions::maximumBlockSize |
Maximum allowed block size.
Matrix blocks with side larger than this value will be split. This can be used to limit the time devoted to (serial) processing of an individual block, especially when a large number of threads is used.
Default value: UINT_MAX.
| unsigned int Bempp::AcaOptions::maximumRank |
Maximum rank of blocks stored in the low-rank format.
Blocks judged to have higher rank will be stored in the dense format.
Default value: UINT_MAX.
| unsigned int Bempp::AcaOptions::minimumBlockSize |
Minimum size of blocks approximated with ACA.
Matrix blocks whose smaller side is less than this value will be stored in the dense format (ACA will not be attempted on these blocks).
Default value: 16.
| AcaAssemblyMode Bempp::AcaOptions::mode |
ACA assembly mode.
This parameter lets you choose between three ways of discretizing operators using ACA. Suppose you have an integral operator 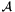 that you want to discretize using a test space
that you want to discretize using a test space 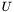 and and trial space
and and trial space 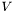 .
.
mode is set to GLOBAL_ASSEMBLY (default), ACA is used in the most straightforward way possible, i.e. to approximate blocks of the operator 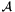 discretized with the basis functions of
discretized with the basis functions of 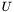 and
and 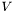 .
.If mode is set to LOCAL_ASSEMBLY, the discretization 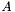 of
of 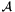 is constructed as a sum
is constructed as a sum
![\[ A = \sum_{i=1}^n \alpha_i P_i A_i Q_i, \]](form_33.png)
where 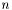 is a small integer,
is a small integer, 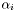 scalar coefficients,
scalar coefficients, 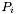 and
and 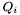 sparse matrices and
sparse matrices and 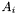 H-matrices representing integral operators discretized with basis functions whose support extends over single elements only (for example functions linear on a single element and zero everywhere else). In most practical cases all matrices
H-matrices representing integral operators discretized with basis functions whose support extends over single elements only (for example functions linear on a single element and zero everywhere else). In most practical cases all matrices 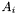 are equal (and obviously only a single copy is stored in memory). This assembly mode takes advantage of the fact that ACA becomes more efficient as the support of test and trial functions is reduced. Thus, assembly in LOCAL_ASSEMBLY mode is often much faster than in GLOBAL_ASSEMBLY mode. However, this comes at the price of increased memory use, since the matrices
are equal (and obviously only a single copy is stored in memory). This assembly mode takes advantage of the fact that ACA becomes more efficient as the support of test and trial functions is reduced. Thus, assembly in LOCAL_ASSEMBLY mode is often much faster than in GLOBAL_ASSEMBLY mode. However, this comes at the price of increased memory use, since the matrices 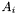 are typically much bigger than
are typically much bigger than 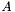 . In addition, the DiscreteBoundaryOperator::asDiscreteAcaBoundaryOperator() function is not currently implemented for products of operators, so discrete operators created in the
. In addition, the DiscreteBoundaryOperator::asDiscreteAcaBoundaryOperator() function is not currently implemented for products of operators, so discrete operators created in the LOCAL_ASSEMBLY modes cannot be converted into single H-matrices. Thus, they cannot be used for H-LU preconditioning.
More information about the matrices 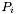 and
and 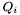 can be found in the documentation of the SyntheticIntegralOperator class. See also the documentation of non-member constructors of particular integral operators, such as laplace3dSingleLayerBoundaryOperator() and helmholtz3dHypersingularBoundaryOperator(), for explicit expressions used to represent these operators in the
can be found in the documentation of the SyntheticIntegralOperator class. See also the documentation of non-member constructors of particular integral operators, such as laplace3dSingleLayerBoundaryOperator() and helmholtz3dHypersingularBoundaryOperator(), for explicit expressions used to represent these operators in the LOCAL_ASSEMBLY mode.
The HYBRID_ASSEMBLY mode is available for operators whose weak form can be written as
![\[ \int_\Gamma \int_\Sigma f(x) \, K(x, y) \, g(y) \, \mathrm{d}\Gamma(x) \,\mathrm{d}\Sigma(y), \]](form_38.png)
where 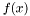 and
and 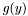 are scalar basis functions of
are scalar basis functions of 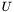 and
and 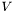 (not any transformations of them, i.e. not their surface curls, divs etc.), *at least as long as the supports of
(not any transformations of them, i.e. not their surface curls, divs etc.), *at least as long as the supports of 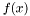 and
and 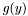 do not overlap*. (Note that this is possible—for
do not overlap*. (Note that this is possible—for 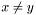 —even for hypersingular operators.) In this mode, individual blocks of the operator are assembled differently, depending on whether the bounding box of the supports of the test basis functions contributing to a given block overlaps or not with the bounding box of the supports of the trial basis functions.
—even for hypersingular operators.) In this mode, individual blocks of the operator are assembled differently, depending on whether the bounding box of the supports of the test basis functions contributing to a given block overlaps or not with the bounding box of the supports of the trial basis functions.
Blocks for which these two boxes overlap are assembled as in the GLOBAL_ASSEMBLY mode, using an arbitrary weak form (possibly one that does not have the form defined above). For the remaining blocks, ACA is used to approximate the discretization of the weak form as defined above with test and trial functions taken as the restrictions of the the basis functions of 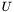 and
and 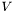 to single elements. After the assembly of each such block, linear combinations of its rows and columns are used to build a low-rank representation of the block in the original bases of
to single elements. After the assembly of each such block, linear combinations of its rows and columns are used to build a low-rank representation of the block in the original bases of 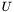 and
and 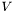 .
.
This mode combines the advantages of LOCAL_ASSEMBLY (fast matrix construction) and GLOBAL_ASSEMBLY (low memory consumption, representation in the form of a single H-matrix). However, at present it cannot be used for Maxwell operators, which require vector basis functions.
Some integral operators may not support the LOCAL_ASSEMBLY and HYBRID_ASSEMBLY modes. How these operators behave when one of these modes is chosen can be controlled with the reactionToUnsupportedMode parameter.
Referenced by Bempp::SyntheticIntegralOperator< BasisFunctionType_, ResultType_ >::getContextsForInternalAndAuxiliaryOperators(), Bempp::laplace3dAdjointDoubleLayerBoundaryOperator(), Bempp::laplace3dDoubleLayerBoundaryOperator(), Bempp::laplace3dHypersingularBoundaryOperator(), Bempp::laplace3dSingleLayerBoundaryOperator(), Bempp::maxwell3dSingleLayerBoundaryOperator(), Bempp::modifiedHelmholtz3dAdjointDoubleLayerBoundaryOperator(), Bempp::modifiedHelmholtz3dDoubleLayerBoundaryOperator(), Bempp::modifiedHelmholtz3dHypersingularBoundaryOperator(), Bempp::modifiedHelmholtz3dSingleLayerBoundaryOperator(), and Bempp::AssemblyOptions::switchToAcaMode().
| std::string Bempp::AcaOptions::outputFname |
| bool Bempp::AcaOptions::outputPostscript |
If true, hierarchical matrix structure will be written in PostScript format at the end of the assembly procedure.
Default value: false.
| ReactionToUnsupportedMode Bempp::AcaOptions::reactionToUnsupportedMode |
Action to take when an unsupported assembly mode is detected.
This parameter controls what happens if an integral operator is requested to construct its discrete weak form in an ACA mode (LOCAL_ASSEMBLY or HYBRID_ASSEMBLY) it does not support.
If reactionToUnsupportedMode is set to IGNORE, the operator silently assembles its discrete weak form in the GLOBAL_ASSEMBLY mode.
It reactionToUnsupportedMode is set to WARNING (default), the operator emits a warning message to the standard output and assembles its discrete weak form in the GLOBAL_ASSEMBLY mode.
If reactionToUnsupportedMode is set to ERROR, the operator throws an exception.
Referenced by Bempp::AssemblyOptions::switchToAcaMode().
| bool Bempp::AcaOptions::recompress |
Recompress ACA matrix after construction?
If true, blocks of H matrices are agglomerated in an attempt to reduce memory consumption.
Warning: this procedure is not parallelised yet, therefore it may be slow.
Default value: false.
| double Bempp::AcaOptions::scaling |
Estimate of the magnitude of typical entries of the matrix to be approximated.
Usually does not need to be changed. Default value: 1.
Referenced by Bempp::WeakFormAcaAssemblyHelper< BasisFunctionType, ResultType >::scale().
| bool Bempp::AcaOptions::useAhmedAca |
Choice of ACA variant.
If true, the default implementation of the ACA algorithm from the AHMED library will be used.
If false, an alternative formulation of ACA will be used. This formulation appears to be more successful in the approximation of operators whose matrices contain empty blocks (like the double-layer boundary operator for the Laplace equation) and in general it tries harder to find a low-rank approximation of a block before falling back to a dense representation.
Default value: false.
 1.8.5
1.8.5